
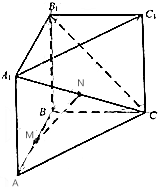
 如圖,三棱柱ABC-A1B1C1中,側(cè)棱與底面垂直,AB⊥BC,AB=BC=BB1=2,M,N分別是AB,A1C的中點(diǎn).
如圖,三棱柱ABC-A1B1C1中,側(cè)棱與底面垂直,AB⊥BC,AB=BC=BB1=2,M,N分別是AB,A1C的中點(diǎn).分析 (1)欲證MN||平面BCC1B1,根據(jù)直線與平面平行的判定定理只需證MN與平面BCC1B1內(nèi)一直線平行即可,
連接BC1,AC1,根據(jù)中位線定理知MN||BC1,由此證明MN∥平面BCC1B1;
(2)以B為原點(diǎn),BA為x軸,BC為y軸,BB1為z軸建立空間直角坐標(biāo)系,求出平面A1B1C的法向量$\overrightarrow{n}$=(x,y,z),根據(jù)法向量$\overrightarrow{n}$∥$\overrightarrow{MN}$可知MN⊥平面A1B1C;
(3)MN是三棱錐M-ABC1的高,底面△ABC1是直角三角形,由此求出三棱錐的體積.
解答  解:(1)證明:連接BC1,AC1,
解:(1)證明:連接BC1,AC1,
在△ABC1中,M,N是AB,A1C的中點(diǎn),
∴MN||BC1;
又MN?平面BCC1B1,MN?平面BCC1B1,
∴MN||平面BCC1B1;
(2)證明:如圖,
以B為原點(diǎn)建立空間直角坐標(biāo)系B-xyz,
則B(0,0,0),C(0,2,0),A1(2,0,2),
M(1,0,0),N(1,1,1),B1(0,0,2);
∴$\overrightarrow{{B}_{1}C}$=(0,2,-2),$\overrightarrow{{{A}_{1}B}_{1}}$=(-2,0,0),
$\overrightarrow{NM}$=(0,1,1);
設(shè)平面A1B1C的法向量為$\overrightarrow{n}$=(x,y,z),則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{B}_{1}C}=0}\\{\overrightarrow{n}•\overrightarrow{{{A}_{1}B}_{1}}=0}\end{array}\right.$
令z=1,則x=0,y=1,∴$\overrightarrow{n}$=(0,1,1).
∴$\overrightarrow{n}$=$\overrightarrow{NM}$,即MN⊥平面A1B1C;
(3)由(2)知MN是三棱錐M-ABC1的高,
在直角△ABC1中,BC1=2$\sqrt{2}$,∴MN=$\frac{1}{2}$BC1=$\sqrt{2}$,
A1B1⊥平面BCC1B1,∴A1B1⊥B1C,∴△A1B1C是直角三角形;
∴${S}_{{{△A}_{1}B}_{1}C}$=$\frac{1}{2}$A1B1•B1C=$\frac{1}{2}$×2×2$\sqrt{2}$=2$\sqrt{2}$;
∴三棱錐的體積為
${V}_{三棱錐M{{-A}_{1}B}_{1}C}$=$\frac{1}{3}$${V}_{{{△A}_{1}B}_{1}C}$•MN=$\frac{1}{3}$×2$\sqrt{2}$×$\sqrt{2}$=$\frac{4}{3}$.
點(diǎn)評 本題考查了線面平行和垂直的證明問題,也考查了三棱錐的體積的求法以及空間思維能力和邏輯思維能力的應(yīng)用問題,是綜合性題目.


 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | ①②③ | B. | ①③④ | C. | ②④ | D. | ②③ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com