
分析 (1)當x<0時,-x>0,由已知中當x≥0時,f(x)=x2-2x-1,及函數f(x)是定義在R上的偶函數,可求出當x<0時函數的解析式,進而得到答案,
(2)由二次函數的圖象畫法可得到函數的草圖;根據圖象下降對應函數的單調遞減區間,分析出函數值的取值范圍后可得到答案;
(3)由圖象可得結論.
解答 解:(1)當x<0時,-x>0,f(-x)=x2+2x-1.
∵f(x)是定義在R上的偶函數,∴f(-x)=f(x)
∴f(x)=x2+2x-1--------------------------------------(2分)
∴f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x-1,x≥0}\\{{x}^{2}+2x-1,x<0}\end{array}\right.$--------------------------------3分
(2)函數圖象如圖所示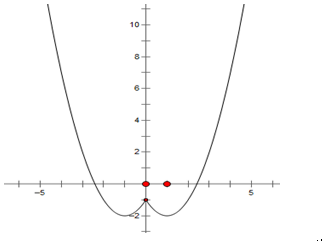
-----------------------------------------------------------------------------------------(5分)
單調減區間為(-∞,-1],[0,1]------------------------------------(6分)
f(x)min=-2,函數沒有最大值(注:不說明最大值情況扣1分)--(8分)
(3)m∈{-2}∪(-1,+∞)----------------------------------------------------------(10分)
點評 本題考查的知識點是函數圖象,函數的單調區間,函數的值域,是函數圖象和性質的綜合應用,難度中檔.


 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:高中數學 來源: 題型:選擇題
| A. | {x|-1<x<1} | B. | {x|-1≤x<2} | C. | {x|1≤x<2} | D. | {x|-1≤x≤1} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
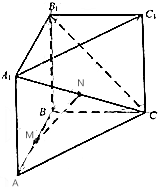 如圖,三棱柱ABC-A1B1C1中,側棱與底面垂直,AB⊥BC,AB=BC=BB1=2,M,N分別是AB,A1C的中點.
如圖,三棱柱ABC-A1B1C1中,側棱與底面垂直,AB⊥BC,AB=BC=BB1=2,M,N分別是AB,A1C的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com