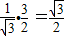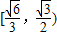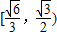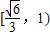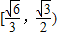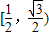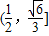已知正△ABC的頂點A在平面α上,頂點B、C在平面α的同一側,D為BC的中點,若△ABC在平面α上的投影是以A為直角頂點的三角形,則直線AD與平面α所成角的正弦值的范圍為 .
【答案】
分析:根據題意,作圖,設正三角形的邊長為1,設出B,C到面的距離分別為a,b,,則DG的長度為兩者和的一半,通過解直角三角形用a,b表示出DG,得出sinα的表達式后,再根據條件,利用函數、不等式知識研究其最值.
解答: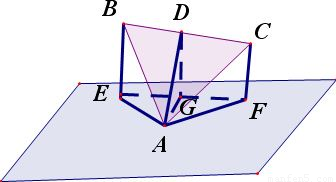
解:設正△ABC邊長為1,則線段AD=
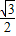
設B,C到平面α距離分別為a=BE,b=CF,
則D到平面α距離為hDG=
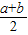
射影三角形兩直角邊的平方分別為1-a
2,1-b
2,
設線段BC射影長為c,則1-a
2+1-b
2=c
2,(1)
又線段AD射影長為
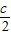
,
所以(
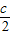
)
2+
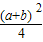
=AD
2=

,(2)
由(1)(2)聯立解得 ab=

,
所以sinα=
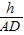
=
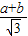
=
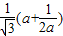
≥
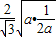
=
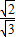
=
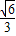
,當a=b=
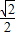
時等號成立.
此時BC與α平行.
令函數f(a)=
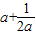
,0<a<1,根據B,C關于D的對稱性,不妨研究
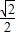
≤a<1的情形.
由于函數f′(a)=1-
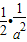
=
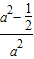
當
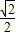
≤a<1時,f′(a)>0,
所以f(a)在(
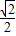
1)上單調遞增,當a趨近于1時,f(a)趨近于1+

=

.,
sinα趨近于
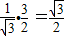
所以sinα的取值范圍為
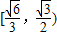
故答案為:
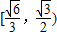 點評:
點評:本題考查線面角的大小度量,考查空間想象、計算、推理論證能力.以及建立數學模型,解決數學模型的能力.

 解:設正△ABC邊長為1,則線段AD=
解:設正△ABC邊長為1,則線段AD=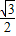
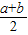
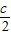 ,
,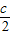 )2+
)2+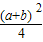 =AD2=
=AD2= ,(2)
,(2) ,
,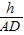 =
=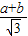 =
=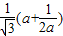 ≥
≥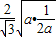 =
=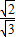 =
=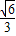 ,當a=b=
,當a=b=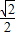 時等號成立.
時等號成立.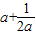 ,0<a<1,根據B,C關于D的對稱性,不妨研究
,0<a<1,根據B,C關于D的對稱性,不妨研究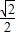 ≤a<1的情形.
≤a<1的情形.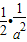 =
=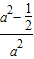
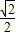 ≤a<1時,f′(a)>0,
≤a<1時,f′(a)>0,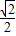 1)上單調遞增,當a趨近于1時,f(a)趨近于1+
1)上單調遞增,當a趨近于1時,f(a)趨近于1+ =
= .,
.,