【題目】已知橢圓
的中心為
，左、右焦點分別為
、
，上頂點為
，右頂點為
，且
、
、
成等比數列.
（1）求橢圓的離心率；
（2）判斷
的形狀，并說明理由.
備戰中考寒假系列答案科目：高中數學 來源： 題型：
【題目】設橢圓
，定義橢圓
的“相關圓
”的方程為
，若拋物線
的焦點與橢圓的一個焦點重合，且橢圓短軸的一個端點和其兩個焦點構成直角三角形.
（1）求橢圓的方程和“相關圓”的方程；
（2）若直線
與圓相切，且與橢圓交于
兩點，
為坐標原點.
①求證：
；
②求
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的方程
，焦點為
，已知點
在上，且點到點的距離比它到
軸的距離大1.
（1）試求出拋物線的方程；
（2）若拋物線上存在兩動點
（在對稱軸兩側），滿足
（
為坐標原點），過點作直線交于
兩點，若
，線段
上是否存在定點
，使得
恒成立？若存在，請求出的坐標，若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
，
，其中
恒不為0.
（1）設
，求函數
在x＝1處的切線方程；
（2）若
是函數與
的公共極值點，求證：存在且唯一；
（3）設
，是否存在實數a，b，使得
在(0，
)上恒成立？若存在，請求出實數a，b滿足的條件；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空氣質量指數AQI是反映空氣質量狀況的指數，AQI指數值越小，表明空氣質量越好，其對應關系如下表：
AQI指數值 | 0～50 | 51～100 | 101～150 | 151～200 | 201～300 | ＞300 |
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
下圖是某市10月1日—20日AQI指數變化趨勢：
下列敘述錯誤的是
A. 這20天中AQI指數值的中位數略高于100
B. 這20天中的中度污染及以上的天數占
C. 該市10月的前半個月的空氣質量越來越好
D. 總體來說，該市10月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】科赫曲線是一種外形像雪花的幾何曲線，一段科赫曲線可以通過下列操作步驟構造得到．任畫一條線段，然后把它均分成三等分，以中間一段為邊向外作正三角形，并把“中間一段”去掉，這樣，原來的條線段就變成了4條小線段構成的折線，稱為“一次構造”；用同樣的方法把每一條小線段重復上述步驟，得到了16條更小的線段構成的折線，稱為“二次構造”，…，如此進行“
次構造”，就可以得到一條科曲線．若要科赫曲線的長度達到原來的100倍，至少需要通過構造的次數是（ ）．（取
）
A.15B.16C.17D.18
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知在算法中“
”和“
”分別表示取商和取余數.為了驗證三位數卡普雷卡爾“數字黑洞”（即輸入一個無重復數字的三位數，經過如圖的有限次的重排求差計算，結果都為495）.小明輸入
，則輸出的
（ ）
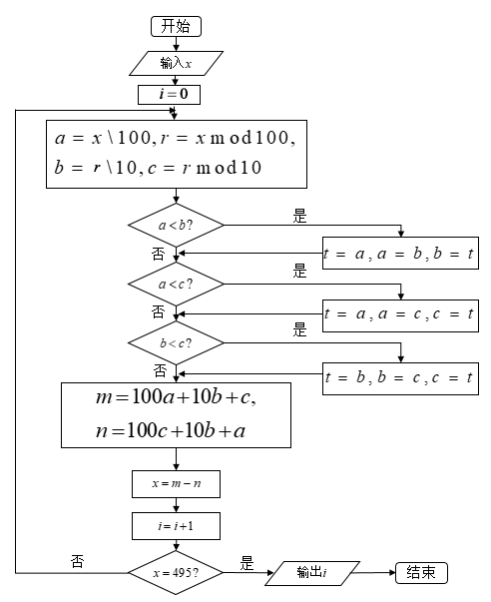
A.3B.4C.5D.6
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列｛
｝的首項a1＝2，前n項和為
，且數列｛
｝是以
為公差的等差數列·
（1）求數列｛｝的通項公式；
（2）設
，
，數列｛
｝的前n項和為
，
①求證：數列｛
｝為等比數列，
②若存在整數m，n(m＞n＞1)，使得
，其中
為常數，且
－2，求的所有可能值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
