
【題目】如圖,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() ,
,![]() .
.
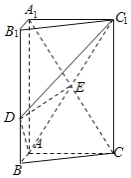
(1)試用空間向量證明直線![]() 與平面
與平面![]() 不平行;
不平行;
(2)設平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() ,若
,若![]() ,求
,求![]() 的長;
的長;
(3)在(2)的條件下,設平面![]() 平面
平面![]() ,求直線
,求直線![]() 與平面
與平面![]() 的所成角.
的所成角.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
可建立空間直角坐標系![]() ,設
,設![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)由![]() 平面
平面![]() 可知
可知![]() ,0,
,0,![]() ,為平面
,為平面![]() 的一個法向量,
的一個法向量,![]() ,
,![]() 即可判定;
即可判定;
(2)求出平面![]() 的法向量,利用平面
的法向量,利用平面![]() 與平面
與平面![]() 所成的銳二面角為
所成的銳二面角為![]() ,
,![]() ,建立方程,即可求得結論.
,建立方程,即可求得結論.
(3)在(2)的條件下,求出直線![]() 的方向向量,平面
的方向向量,平面![]() 的一個法向量,代入向量夾角公式,可得答案.
的一個法向量,代入向量夾角公式,可得答案.
解:依題意建立如圖所示的空間直角坐標系![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(1)證明:由![]() 平面
平面![]() ,知
,知![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
![]()
所以![]()
即直線![]() 與平面
與平面![]() 不平行
不平行
(2)平面![]() 的法向量
的法向量![]() ,則
,則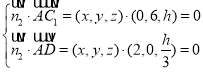
取![]() ,則
,則![]() ,故
,故![]()
所以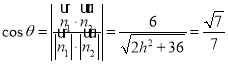
解得![]()
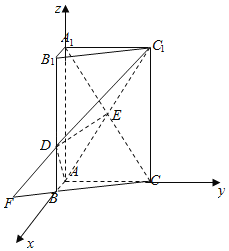
(3)在平面![]() 內,分別延長
內,分別延長![]() ,交于點
,交于點![]() ,連接
,連接![]() ,則直線
,則直線![]() 是平面
是平面![]() 與平面
與平面![]() 交線,
交線,
![]() ,
,![]()
![]()
![]() ,
,
![]() ,
,
![]()
設直線![]() 與平面
與平面![]() 的所成的角是
的所成的角是![]() ,則
,則![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
![]()
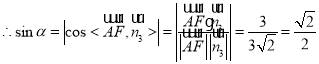
![]()
![]() 直線
直線![]() 與平面
與平面![]() 的所成角為
的所成角為![]() .
.


科目:高中數學 來源: 題型:
【題目】![]() 兩地相距
兩地相距![]() 千米,汽車從
千米,汽車從![]() 地勻速行駛到
地勻速行駛到![]() 地,速度不超過
地,速度不超過![]() 千米小時,已知汽車每小時的運輸成本(單位:元)由可變部分和固定部分兩部分組成:可變部分與速度
千米小時,已知汽車每小時的運輸成本(單位:元)由可變部分和固定部分兩部分組成:可變部分與速度![]() 的平方成正比,比例系數為
的平方成正比,比例系數為![]() ,固定部分為
,固定部分為![]() 元,
元,
(1)把全程運輸成本![]() (元)表示為速度
(元)表示為速度![]() (千米小時)的函效:并求出當
(千米小時)的函效:并求出當![]() 時,汽車應以多大速度行駛,才能使得全程運輸成本最小;
時,汽車應以多大速度行駛,才能使得全程運輸成本最小;
(2)隨著汽車的折舊,運輸成本會發生一些變化,那么當![]() ,此時汽車的速度應調整為多大,才會使得運輸成本最小,
,此時汽車的速度應調整為多大,才會使得運輸成本最小,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】棋盤上標有第![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 站,棋子開始位于第
站,棋子開始位于第![]() 站,棋手拋擲均勻硬幣走跳棋游戲,若擲出正面,棋子向前跳出一站;若擲出反面,棋子向前跳出兩站,直到調到第
站,棋手拋擲均勻硬幣走跳棋游戲,若擲出正面,棋子向前跳出一站;若擲出反面,棋子向前跳出兩站,直到調到第![]() 站或第
站或第![]() 站時,游戲結束.設棋子位于第
站時,游戲結束.設棋子位于第![]() 站的概率為
站的概率為![]() .
.
(1)當游戲開始時,若拋擲均勻硬幣![]() 次后,求棋手所走步數之和
次后,求棋手所走步數之和![]() 的分布列與數學期望;
的分布列與數學期望;
(2)證明:![]() ;
;
(3)求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年高考剛過,為了解考生對全國2卷數學試卷難度的評價,隨機抽取了某學校50名男考生與50名女考生,得到下面的列聯表:
非常困難 | 一般 | |
男考生 | 20 | 30 |
女考生 | 40 | 10 |
(1)分別估計該學校男考生、女考生覺得全國2卷數學試卷非常困難的概率;
(2)從該學校隨機抽取3名男考生,2名女考生,求恰有4名考生覺得全國2卷數學試卷非常困難的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() (
(![]() 是常數,且
是常數,且![]() )滿足條件:
)滿足條件:![]() ,且方程
,且方程![]() 有兩個相等實根.
有兩個相等實根.
(1)求![]() 的解析式;
的解析式;
(2)是否存在實數![]() ,使
,使![]() 的定義域和值域分別為
的定義域和值域分別為![]() 和
和![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次綜合素質測試中,共設有40個考室,每個考室30名考生.在考試結束后,為調查其測試前的培訓輔導情況與測試成績的相關性,抽取每個考室中座位號為05的考生,統計了他們的成績,得到如圖所示的頻率分布直方圖.
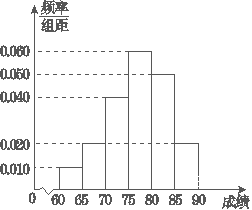
(1)在這個調查采樣中,采用的是什么抽樣方法?
(2)估計這次測試中優秀(80分及以上)的人數;
(3)寫出這40名考生成績的眾數、中位數、平均數的估計值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4—4:坐標系與參數方程]:在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (t為參數,
(t為參數,![]() ),以坐標原點為極點,以x軸的非負半軸為極軸,建立極坐標系,曲線C的極坐標方程為
),以坐標原點為極點,以x軸的非負半軸為極軸,建立極坐標系,曲線C的極坐標方程為![]() ,已知直線
,已知直線![]() 與曲線C交于不同的兩點A,B.
與曲線C交于不同的兩點A,B.
(1)求直線![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)設P(1,2),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前,國內很多評價機構經過反復調研論證,研制出“增值評價”方式。下面實例是某市對“增值評價”的簡單應用,該市教育評價部門對本市![]() 所高中按照分層抽樣的方式抽出
所高中按照分層抽樣的方式抽出![]() 所(其中,“重點高中”
所(其中,“重點高中”![]() 所分別記為
所分別記為![]() ,“普通高中”
,“普通高中”![]() 所分別記為
所分別記為![]() ),進行跟蹤統計分析,將
),進行跟蹤統計分析,將![]() 所高中新生進行了統的入學測試高考后,該市教育評價部門將人學測試成績與高考成績的各校平均總分繪制成了雷達圖.
所高中新生進行了統的入學測試高考后,該市教育評價部門將人學測試成績與高考成績的各校平均總分繪制成了雷達圖.![]() 點表示
點表示![]() 學校入學測試平均總分大約
學校入學測試平均總分大約![]() 分,
分,![]() 點表示
點表示![]() 學校高考平均總分大約
學校高考平均總分大約![]() 分,則下列敘述不正確的是( )
分,則下列敘述不正確的是( )

A.各校人學統一測試的成績都在![]() 分以上
分以上
B.高考平均總分超過![]() 分的學校有
分的學校有![]() 所
所
C.![]() 學校成績出現負增幅現象
學校成績出現負增幅現象
D.“普通高中”學生成績上升比較明顯
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com