解:(1)由f(2)=1得2a+b=2,又x=0一定是方程
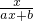
=x的解,
所以

=1無解或有解為0,(3分)
若無解,則ax+b=1無解,得a=0,矛盾,
若有解為0,則b=1,所以a=

. (6分)
(2)f(x)=

,設存在常數m,使得對定義域中任意的x,f(x)+f(m-x)=4恒成立,
取x=0,則f(0)+f(m-0)=4,即
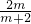
=4,m=-4(必要性)(8分)
又m=-4時,f(x)+f(-4-x)=
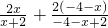
=…=4成立(充分性) (10分)
所以存在常數m=-4,使得對定義域中任意的x,f(x)+f(m-x)=4恒成立,(11分)
(3)|AP|
2=(x+3)
2+(
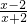
)
2,設x+2=t,t≠0,(13分)
則|AP|
2=(t+1)
2+(
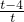
)
2=t
2+2t+2-
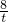
+
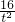
=(t
2+
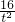
)+2(t-

)+2=(t-

)
2+2(t-

)+10
=( t-

+1)
2+9,(16分)
所以當t-

+1=0時即t=
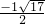
,也就是x=
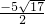
時,
|AP|
min=3 (18分)
分析:(1)根據方程f(x)=x,可知x=0一定是方程
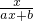
=x的解,從而有方程

=1無解或有解為0,再進行分類討論,可求a、b的值;
(2)由(1)知f(x)=

,假設存在常數m,使得對定義域中任意的x,f(x)+f(m-x)=4恒成立,賦值x=0,,可求參數m的值,再驗證此時等式恒成立即可;
(3)先表示出|AP|
2,再利用換元法,求解時整體考慮,利用配方法求解
點評:本題的考點是恒成立問題,主要考查方程解的問題,考查利用賦值法求解恒成立問題,考查函數的最值問題,關鍵是審清題意,合理轉化,注意賦值法求解恒成立問題時,應需要驗證其恒成立.

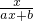 (a,b是非零實常數),滿足f(2)=1,且方程f(x)=x有且僅有一個解.
(a,b是非零實常數),滿足f(2)=1,且方程f(x)=x有且僅有一個解.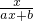 =x的解,
=x的解, =1無解或有解為0,(3分)
=1無解或有解為0,(3分) . (6分)
. (6分) ,設存在常數m,使得對定義域中任意的x,f(x)+f(m-x)=4恒成立,
,設存在常數m,使得對定義域中任意的x,f(x)+f(m-x)=4恒成立,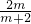 =4,m=-4(必要性)(8分)
=4,m=-4(必要性)(8分)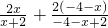 =…=4成立(充分性) (10分)
=…=4成立(充分性) (10分)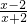 )2,設x+2=t,t≠0,(13分)
)2,設x+2=t,t≠0,(13分)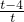 )2=t2+2t+2-
)2=t2+2t+2-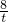 +
+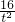 =(t2+
=(t2+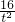 )+2(t-
)+2(t- )+2=(t-
)+2=(t- )2+2(t-
)2+2(t- )+10
)+10 +1)2+9,(16分)
+1)2+9,(16分) +1=0時即t=
+1=0時即t=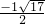 ,也就是x=
,也就是x=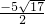 時,
時,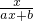 =x的解,從而有方程
=x的解,從而有方程 =1無解或有解為0,再進行分類討論,可求a、b的值;
=1無解或有解為0,再進行分類討論,可求a、b的值; ,假設存在常數m,使得對定義域中任意的x,f(x)+f(m-x)=4恒成立,賦值x=0,,可求參數m的值,再驗證此時等式恒成立即可;
,假設存在常數m,使得對定義域中任意的x,f(x)+f(m-x)=4恒成立,賦值x=0,,可求參數m的值,再驗證此時等式恒成立即可;
