【題目】工廠需要建造一個倉庫，根據市場調研分析，運費與工廠和倉庫之間的距離成正比，倉儲費與工廠和倉庫之間的距離成反比，當工廠和倉庫之間的距離為4千米時，運費為20萬元，倉儲費為5萬元.求：工廠和倉庫之間的距離為多少千米時，運費與倉儲費之和最小，最小為多少萬元.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】在
中，滿足：
，M是
的中點.
（1）若
，求向量
與向量
的夾角的余弦值；
（2）若O是線段
上任意一點，且
，求
的最小值：
（3）若點P是
內一點，且
，
，
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數
，若
滿足
，則稱為函數
的一階不動點，若滿足
，則稱為函數的二階不動點，若滿足，且
，則稱為函數的二階周期點.
（1）設
.
①當
時，求函數的二階不動點，并判斷它是否是函數數的二階周期點；
②已知函數存在二階周期點，求k的值；
（2）若對任意實數b，函數
都存在二階周期點，求實數c的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，以坐標原點O為極點，x軸的非負半軸為極軸建立極坐標系，直線l的極坐標方程為
，曲線C的參數方程為
(
為參數，
)．
(1)求直線l的直角坐標方程及曲線C的普通方程；
(2)證明：直線l和曲線C相交，并求相交弦的長度．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
,
是函數
圖象上的任意兩點,且角
的終邊經過點
,若
時,
的最小值為
．
（1）求函數
的解析式；
（2）若方程
在
內有兩個不同的解,求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，底面ABCD是正方形，且
，平面PCD⊥平面ABCD，
，點E為線段PC的中點，點F是線段AB上的一個動點.
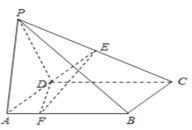
（1）求證：平面
平面PBC；
（2）設二面角
的平面角為
，試判斷在線段AB上是否存在這樣的點F，使得
，若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
函數
（1）當
時，解不等式
（2）若關于
的方程
的解集中怡好有一個元素，求
的取值范圍；
（3）設
若對任意
函數
在區間
上的最大值與最小值的差不超過1，求的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
