
(本題滿分16分)
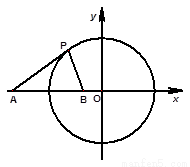
已知圓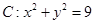 ,點
,點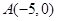 ,直線
,直線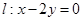 .
.
⑴求與圓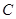 相切,且與直線
相切,且與直線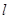 垂直的直線方程;
垂直的直線方程;
⑵在直線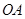 上(
上(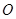 為坐標原點),存在定點
為坐標原點),存在定點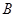 (不同于點
(不同于點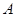 ),滿足:對于圓
),滿足:對于圓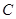 上任一點
上任一點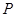 ,都有
,都有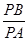 為一常數(shù),試求所有滿足條件的點
為一常數(shù),試求所有滿足條件的點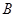 的坐標.
的坐標.
(1)直線方程為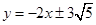
(2)存在點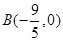 對于圓
對于圓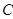 上任一點
上任一點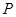 ,都有
,都有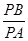 為常數(shù)
為常數(shù)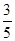 。
。
【解析】解:⑴設(shè)所求直線方程為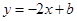 ,即
,即 ,
,
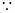 直線與圓相切,∴
直線與圓相切,∴ ,得
,得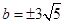 ,
,
∴所求直線方程為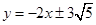 -----------5分
-----------5分
⑵方法1:假設(shè)存在這樣的點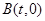 ,
,
當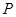 為圓
為圓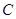 與
與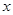 軸左交點
軸左交點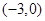 時,
時,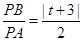 ;
;
當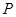 為圓
為圓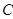 與
與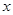 軸右交點
軸右交點 時,
時,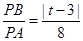 ,
,
依題意,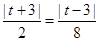 ,解得,
,解得,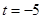 (舍去),或
(舍去),或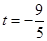 。 -----------------8分
。 -----------------8分
下面證明 點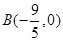 對于圓
對于圓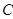 上任一點
上任一點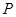 ,都有
,都有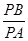 為一常數(shù)。
為一常數(shù)。
設(shè)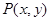 ,則
,則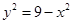 ,
,
∴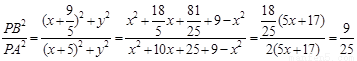 ,
,
從而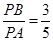 為常數(shù)。
-------------15分
為常數(shù)。
-------------15分
方法2:假設(shè)存在這樣的點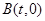 ,使得
,使得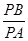 為常數(shù)
為常數(shù)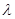 ,則
,則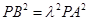 ,
,
∴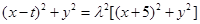 ,將
,將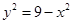 代入得,
代入得,
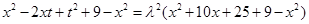 ,即
,即
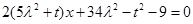 對
對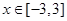 恒成立, ----------------8分
恒成立, ----------------8分
∴ ,解得
,解得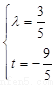 或
或 (舍去),
(舍去),
所以存在點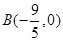 對于圓
對于圓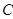 上任一點
上任一點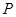 ,都有
,都有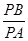 為常數(shù)
為常數(shù)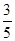 。 ------------15分
。 ------------15分


科目:高中數(shù)學 來源: 題型:
| a1+2a2+3a3+…+nan |
| 1+2+3+…+n |
| n(n+1)(2n+1) |
| 6 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(本題滿分16分)本題共有2個小題,第1小題滿分8分,第2小題滿分8分.
已知函數(shù)![]() (
(![]() ,
,![]() 、
、![]() 是常數(shù),且
是常數(shù),且![]() ),對定義域內(nèi)任意
),對定義域內(nèi)任意![]() (
(![]() 、
、![]() 且
且![]() ),恒有
),恒有![]() 成立.
成立.
(1)求函數(shù)![]() 的解析式,并寫出函數(shù)的定義域;
的解析式,并寫出函數(shù)的定義域;
(2)求![]() 的取值范圍,使得
的取值范圍,使得![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(本題滿分16分)已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .數(shù)列
.數(shù)列![]() 中,
中,![]() ,
,
![]()
![]() .(1)求數(shù)列
.(1)求數(shù)列![]() 的通項公式;(2)若存在常數(shù)
的通項公式;(2)若存在常數(shù)![]() 使數(shù)列
使數(shù)列![]() 是等比數(shù)列,求數(shù)列
是等比數(shù)列,求數(shù)列![]() 的通項公式;(3)求證:①
的通項公式;(3)求證:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源:江蘇省私立無錫光華學校2009—2010學年高二第二學期期末考試 題型:解答題
本題滿分16分)已知圓內(nèi)接四邊形ABCD的邊長分別為AB = 2,BC = 6,CD = DA = 4;求四邊形ABCD的面積.
查看答案和解析>>
科目:高中數(shù)學 來源:2010年上海市徐匯區(qū)高三第二次模擬考試數(shù)學卷(文) 題型:解答題
(本題滿分16分;第(1)小題5分,第(2)小題5分,第三小題6分)
已知函數(shù) 
(1)判斷并證明 在
在 上的單調(diào)性;
上的單調(diào)性;
(2)若存在 ,使
,使 ,則稱
,則稱 為函數(shù)
為函數(shù) 的不動點,現(xiàn)已知該函數(shù)有且僅有一個不動點,求
的不動點,現(xiàn)已知該函數(shù)有且僅有一個不動點,求 的值;
的值;
(3)若 在
在 上恒成立 , 求
上恒成立 , 求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com