
 圖象上一點(diǎn)
圖象上一點(diǎn) 處
處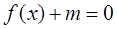 在
在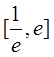 內(nèi)有兩個(gè)不等實(shí)根,求m的取值范圍(其
內(nèi)有兩個(gè)不等實(shí)根,求m的取值范圍(其 為自然對(duì)數(shù)的底數(shù));
為自然對(duì)數(shù)的底數(shù)); 浙大優(yōu)學(xué)小學(xué)年級(jí)銜接捷徑浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級(jí)銜接捷徑浙江大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
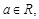 函數(shù)
函數(shù)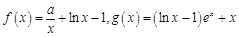
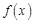 在
在 上的單調(diào)性;
上的單調(diào)性;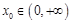 ,使曲線
,使曲線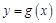 在點(diǎn)
在點(diǎn)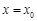 處的切線與
處的切線與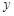 軸垂直?若存在,求出
軸垂直?若存在,求出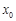 的值;若不存在,請(qǐng)說明理由.
的值;若不存在,請(qǐng)說明理由. 查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
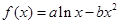 ,
,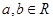 (1)若函數(shù)
(1)若函數(shù)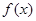 在
在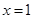 處與直線
處與直線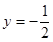 相切;
相切;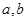 的值; ②求函數(shù)
的值; ②求函數(shù)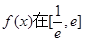 上的最大值;
上的最大值;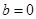 時(shí),若不等式
時(shí),若不等式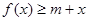 對(duì)所有的
對(duì)所有的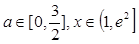 都成立,求實(shí)數(shù)
都成立,求實(shí)數(shù)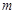 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
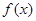 是定義在
是定義在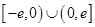 上的奇函數(shù),當(dāng)
上的奇函數(shù),當(dāng)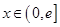 時(shí),
時(shí), 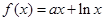 (其中e是自然界對(duì)數(shù)的底,
(其中e是自然界對(duì)數(shù)的底,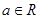 )
)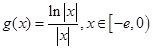 ,求證:當(dāng)
,求證:當(dāng)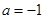 時(shí),
時(shí),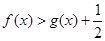 ;
;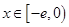 時(shí),
時(shí),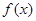 的最小值是3 ?如果存在,求出實(shí)
的最小值是3 ?如果存在,求出實(shí)查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
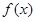 為定義在
為定義在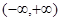 上的可導(dǎo)函數(shù),且
上的可導(dǎo)函數(shù),且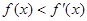 對(duì)于
對(duì)于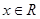 恒成立,設(shè)
恒成立,設(shè)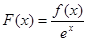 (
(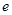 為自然對(duì)數(shù)的底), 則
為自然對(duì)數(shù)的底), 則A.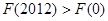 | B.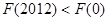 |
C.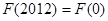 | D.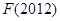 與 與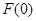 的大小不確定 的大小不確定 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
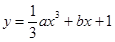 ,其中
,其中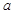 為2,4,6,8中的任意一個(gè),
為2,4,6,8中的任意一個(gè),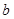 為1,3,5,7中的任意一個(gè)。現(xiàn)從這些曲線中任取兩條,它們?cè)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140823/20140823231152710323.png" style="vertical-align:middle;" />處的切線相互平行的組數(shù)為
為1,3,5,7中的任意一個(gè)。現(xiàn)從這些曲線中任取兩條,它們?cè)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140823/20140823231152710323.png" style="vertical-align:middle;" />處的切線相互平行的組數(shù)為| A.9 | B.10 |
| C.12 | D.14 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
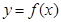 的導(dǎo)函數(shù)
的導(dǎo)函數(shù)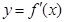 的圖象,
的圖象,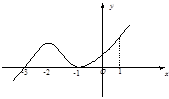
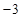 是函數(shù)
是函數(shù)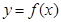 的極值點(diǎn);
的極值點(diǎn);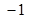 是函數(shù)
是函數(shù)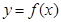 的極小值點(diǎn);
的極小值點(diǎn);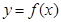 在
在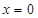 處切線的斜率小于零;
處切線的斜率小于零;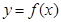 在區(qū)間
在區(qū)間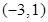 上單調(diào)遞增.則正確命題的序號(hào)是( )
上單調(diào)遞增.則正確命題的序號(hào)是( )| A.①② | B.①④ | C.②③ | D.②④ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com