
 (必修3做) 在一個匣內有大小完全相同的1個白球、2個紅球和2個黑球,現從中任取兩球,分別求下列事件的概率:
(必修3做) 在一個匣內有大小完全相同的1個白球、2個紅球和2個黑球,現從中任取兩球,分別求下列事件的概率: ;(4分)
;(4分) ;(7分)
;(7分) .(10分)
.(10分) (3分)
(3分) ,求得BC=
,求得BC=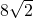 ;(5分)
;(5分)
 ,求得BC=
,求得BC=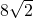 .
.

 新編小學單元自測題系列答案
新編小學單元自測題系列答案 字詞句段篇系列答案
字詞句段篇系列答案科目:高中數學 來源: 題型:
 (必修3做)如圖,大正方形靶盤的邊長為
(必修3做)如圖,大正方形靶盤的邊長為| 13 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (必修3做) 在一個匣內有大小完全相同的1個白球、2個紅球和2個黑球,現從中任取兩球,分別求下列事件的概率:
(必修3做) 在一個匣內有大小完全相同的1個白球、2個紅球和2個黑球,現從中任取兩球,分別求下列事件的概率:查看答案和解析>>
科目:高中數學 來源:2009-2010學年湖南省永州市高一(上)期末數學試卷(解析版) 題型:解答題

查看答案和解析>>
科目:高中數學 來源:2009-2010學年湖南省永州市高一(上)期末數學試卷(解析版) 題型:選擇題
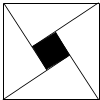
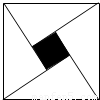 (必修3做)如圖,大正方形靶盤的邊長為
(必修3做)如圖,大正方形靶盤的邊長為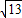 ,四個全等的直角三角形圍成一個小正方形,即陰影部分.較短的直角邊長為2,現向大正方形靶盤投擲飛鏢,則飛鏢落在陰影區域的概率為( )
,四個全等的直角三角形圍成一個小正方形,即陰影部分.較短的直角邊長為2,現向大正方形靶盤投擲飛鏢,則飛鏢落在陰影區域的概率為( )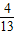
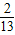
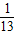
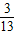
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com