
【題目】在一張足夠大的紙板上截取一個面積為3600平方厘米的矩形紙板ABCD,然后在矩形紙板的四個角上切去邊長相等的小正方形,再把它的邊沿虛線折起,做成一個無蓋的長方體紙盒(如圖).設小正方形邊長為x厘米,矩形紙板的兩邊AB,BC的長分別為a厘米和b厘米,其中a≥b. 
(1)當a=90時,求紙盒側面積的最大值;
(2)試確定a,b,x的值,使得紙盒的體積最大,并求出最大值.
【答案】
(1)解:因為矩形紙板ABCD的面積為3600,故當a=90時,b=40,
從而包裝盒子的側面積S=2×x(90﹣2x)+2×x(40﹣2x)=﹣8x2+260x,x∈(0,20)
因為S=﹣8x2+260x=﹣8(x﹣16.25)2+2112.5,
故當x=16.25時,側面積最大,最大值為2112.5平方厘米
(2)解:包裝盒子的體積V=(a﹣2x)(b﹣2x)x=x[ab﹣2(a+b)x+4x2],x∈(0, ![]() ),b≤60.
),b≤60.
V=x[ab﹣2(a+b)x+4x2]≤x(ab﹣4 ![]() x+4x2)=x(3600﹣240x+4x)
x+4x2)=x(3600﹣240x+4x)
=4x3﹣240x2+3600x.
當且僅當a=b=60時等號成立.
設f(x)=4x3﹣240x2+3600x,x∈(0,30).則f′(x)=12(x﹣10)(x﹣30).
于是當0<x<10時,f′(x)>0,所以f(x)在(0,10)上單調遞增;
當10<x<30時,f′(x)<0,所以f(x)在(10,30)上單調遞減.
因此當x=10時,f(x)有最大值f(10)=16000,此時a=b=60,x=10.
答:當a=b=60,x=10時紙盒的體積最大,最大值為16000立方厘米
【解析】(1)當a=90時,b=40,求出側面積,利用配方法求紙盒側面積的最大值;(2)表示出體積,利用基本不等式,導數知識,即可確定a,b,x的值,使得紙盒的體積最大,并求出最大值.


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】《九章算術》是中國古代的數學專著,其中的“更相減損術”可以用來求兩個數的最大公約數,原文是:可半者半之,不可半者,副置分母、子之數,以少減多,更相減損,求其等也,以等數約之. 翻譯為現代的語言如下:如果需要對分數進行約分,那么可以折半的話,就折半(也就是用2來約分).如果不可以折半的話,那么就比較分母和分子的大小,用大數減去小數,互相減來減去,一直到減數與差相等為止,用這個相等的數字來約分,現給出“更相減損術”的程序框圖如圖所示,如果輸入的![]() ,
,![]() ,則輸出的
,則輸出的![]() ( )
( )

A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的內角A,B,C的內角對邊分別為a,b,c,滿足(a+b+c)(a﹣b+c)=ac.
(1)求B.
(2)若sinAsinC= ![]() ,求C.
,求C.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,D為邊BC上一點,AD=6,BD=3, DC=2.
(1)若AD⊥BC,求∠BAC的大小;
(2)若∠ABC= ![]() ,求△ADC的面積.
,求△ADC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設X~N(1,σ2),其正態分布密度曲線如圖所示,且P(X≥3)=0.0228,那么向正方形OABC中隨機投擲10000個點,則落入陰影部分的點的個數的估計值為( )
(附:隨機變量ξ服從正態分布N(μ,σ2),則P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
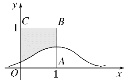
A. 6038 B. 6587 C. 7028 D. 7539
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分12分)袋中裝有黑色球和白色球共7個,從中任取2個球都是白色球的概率為![]() .現有甲、乙兩人從袋中輪流摸出1個球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后終止.每個球在每一次被摸出的機會都是等可能的,用X表示摸球終止時所需摸球的次數.
.現有甲、乙兩人從袋中輪流摸出1個球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后終止.每個球在每一次被摸出的機會都是等可能的,用X表示摸球終止時所需摸球的次數.
(1)求隨機變量X的分布列和均值E(X);
(2)求甲摸到白色球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某漁業公司年初用81萬元購買一艘捕魚船,第一年各種費用為1萬元,以后每年都增加2萬元,每年捕魚收益30萬元.
![]() 問第幾年開始獲利?
問第幾年開始獲利?
![]() 若干年后,有兩種處理方案:方案一:年平均獲利最大時,以46萬元出售該漁船;
若干年后,有兩種處理方案:方案一:年平均獲利最大時,以46萬元出售該漁船;
方案二:總純收入獲利最大時,以10萬元出售該漁船![]() 問:哪一種方案合算?請說明理由.
問:哪一種方案合算?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com