
【題目】如圖,過點P作圓O的割線PBA與切線PE,E為切點,連接AE、BE,∠APE的平分線與AE、BE分別交于點C、D,其中∠AEB=30°. 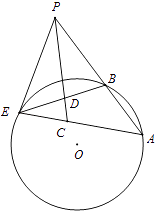
(1)求證: ![]()
(2)求∠PCE的大小.
【答案】
(1)證明:∵PE是圓的切線,∴∠PEB=∠PAC,
∵AE是∠APE的平分線,∴∠EPC=∠APC,
∴△PED∽△PAC,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]()
(2)解:∵PE是圓的切線,∴∠PEB=∠PAC,
∵AE是∠APE的平分線,∴∠EPC=∠APC,
根據三角形的外角與內角關系有:∠EDC=∠PEB+∠EPC;∠ECD=∠PAC+∠APC,
∴∠EDC=∠ECD,∴△EDC為等腰三角形,
又∠AEB=30°,
∴∠EDC=∠ECD=75°,即∠PCE=75°
【解析】(1)證明△PED∽△PAC,結合角平分線的性質,即可證明結論;(2)利用PE是圓的切線,可得∠PEB=∠PAC,利用AE是∠APE的平分線,可得∠EPC=∠APC,根據三角形的外角與內角關系,可得∠EDC=∠ECD,即可得出結論.


科目:高中數學 來源: 題型:
【題目】某電信公司從所在地的1000名使用4G手機用戶中,隨機抽取了20名,對其收集每日使用流量(單位:M)進行統計,得到如下數據:
流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
人數 | 1 | 6 | 6 | 5 | 2 | 0 |
(1)估計這20名4G手機用戶每日使用流量(單位:M)的平均值;
(2)估計此地1000名使用4G手機用戶中每日使用流量不少于10M用戶數;
(3)在15≤x<20和20≤x<25兩組用戶中,隨機抽取兩人作進一步問卷調查,求所抽取的兩人恰好來自不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查喜歡看書是否與性別有關,某校調查小組就“是否喜歡看書”這個問題,在全校隨機調研了100名學生.
(1)完成下列![]() 列聯表:
列聯表:
喜歡看書 | 不喜歡看書 | 合計 | |
女生 | 15 | 50 | |
男生 | 25 | ||
合計 | 100 |
(2)能否在犯錯率不超過0.025的前提下認為“喜歡看書與性別有關”.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一某班的一次數學測試成績的莖葉圖和頻率分布直方圖因故都受到不同程度的損壞,但可見部分如下,據此解答如下問題: 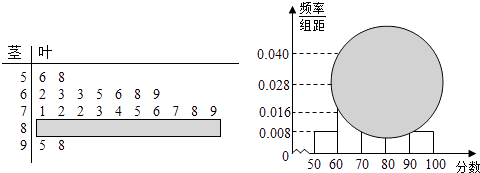
(Ⅰ)求分數在[50,60)的頻率及全班人數;
(Ⅱ)求分數在[80,90)之間的頻數,并計算頻率分布直方圖中[80,90)間的矩形的高;
(Ⅲ)若規定:75(包含75分)分以上為良好,90分(包含90分)以上為優秀,要從分數在良好以上的試卷中任取兩份分析學生失分情況,設在抽取的試卷中,分數為優秀的試卷份數為X,求X的概率分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一某班的一次數學測試成績的莖葉圖和頻率分布直方圖因故都受到不同程度的損壞,但可見部分如下,據此解答如下問題: 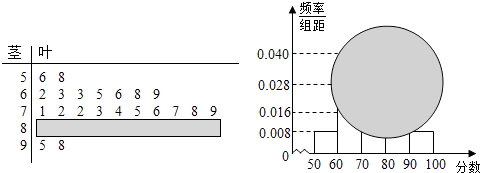
(Ⅰ)求分數在[50,60)的頻率及全班人數;
(Ⅱ)求分數在[80,90)之間的頻數,并計算頻率分布直方圖中[80,90)間的矩形的高;
(Ⅲ)若規定:75(包含75分)分以上為良好,90分(包含90分)以上為優秀,要從分數在良好以上的試卷中任取兩份分析學生失分情況,設在抽取的試卷中,分數為優秀的試卷份數為X,求X的概率分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com