
【題目】已知函數![]() ,其中
,其中![]() 為常數.
為常數.
(1)若![]() ,求函數
,求函數![]() 的極值;
的極值;
(2)若函數![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() ,設函數
,設函數![]() 在
在![]() 上的極值點為
上的極值點為![]() ,求證:
,求證: ![]() .
.
【答案】(1)當![]() 時,
時, ![]() 的極大值為
的極大值為![]() ,無極小值;(2)
,無極小值;(2) ![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】試題分析:(1)求導,利用導函數的符號變化得到函數的單調性,進而得到函數的極值;(2)求導,將函數在某區間上單調遞增轉化為導函數非負恒成立,分離參數,構造函數,將不等式恒成立問題轉化為求函數的最值問題;(3)連續兩次求導,分別通過研究導函數的符號變化研究函數的極值,再作差構造函數,將不等式恒成立問題轉化為求函數的最值問題,再利用求導進行求解.
試題解析:(1)當![]() 時,
時, ![]() ,定義域為
,定義域為![]() ,
,
![]() ,令
,令![]() ,得
,得![]() .
.
|
|
|
|
|
|
|
|
|
| 極大值 |
|
![]() 當
當![]() 時,
時, ![]() 的極大值為
的極大值為![]() ,無極小值.
,無極小值.
(2)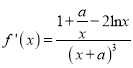 ,由題意
,由題意![]() 對
對![]() 恒成立.
恒成立.
![]()
![]() ,
, ![]() ,
,
![]()
![]() 對
對![]() 恒成立,
恒成立,
![]()
![]() 對
對![]() 恒成立.
恒成立.
令![]() ,
, ![]() ,則
,則![]() ,
,
①若![]() ,即
,即![]() ,則
,則![]() 對
對![]() 恒成立,
恒成立,
![]()
![]() 在
在![]() 上單調遞減,
上單調遞減,
則![]() ,
, ![]() ,
, ![]() 與
與![]() 矛盾,舍去;
矛盾,舍去;
②若![]() ,即
,即![]() ,令
,令![]() ,得
,得![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() 單調遞減,
單調遞減,
當![]() 時,
時, ![]() ,
, ![]() 單調遞增,
單調遞增,
![]() 當
當![]() 時,
時, 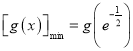
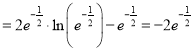 ,
,
![]() .綜上
.綜上![]() .
.
(3)當![]() 時,
時, ![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
則![]()
![]() ,令
,令![]() ,得
,得![]() ,
,
①當![]() 時,
時, ![]() ,
, ![]() 單調遞減,
單調遞減, 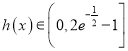 ,
,
![]() 恒成立,
恒成立, ![]() 單調遞減,且
單調遞減,且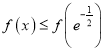 .
.
②當![]() 時,
時, ![]() ,
, ![]() 單調遞增,
單調遞增,
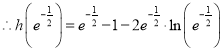
![]()
又![]()
![]() ,
,
![]() 存在唯一
存在唯一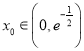 ,使得
,使得![]() ,
, ![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() 單調遞增,
單調遞增,
當![]() 時,
時, ![]() ,
, ![]() 單調遞減,且
單調遞減,且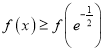 ,
,
由①和②可知, ![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 上單調遞減,
上單調遞減,
![]() 當
當![]() 時,
時, ![]() 取極大值.
取極大值.
![]() ,
, ![]() ,
,
![]()
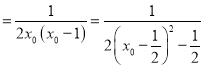 ,
,
又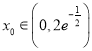 ,
, ![]() ,
, 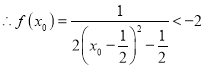 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn,若S9=81,a3+a5=14.
(1)求數列{an}的通項公式;
(2)設bn=![]() ,若{bn}的前n項和為Tn,證明:Tn<
,若{bn}的前n項和為Tn,證明:Tn<![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若關于x的不等式e2x﹣alnx![]() a恒成立,則實數a的取值范圍是( )
a恒成立,則實數a的取值范圍是( )
A.[0,2e]B.(﹣∞,2e]C.[0,2e2]D.(﹣∞,2e2]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,過點
,過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,交圓
兩點,交圓![]() 于
于![]() 兩點(
兩點(![]() 兩點相鄰).
兩點相鄰).
(Ⅰ)若![]() ,當
,當![]() 時,求
時,求![]() 的取值范圍;
的取值范圍;
(Ⅱ)過![]() 兩點分別作曲線
兩點分別作曲線![]() 的切線
的切線![]() ,兩切線交于點
,兩切線交于點![]() ,求
,求![]() 與
與![]() 面積之積的最小值.
面積之積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業欲做一個介紹企業發展史的銘牌,銘牌的截面形狀是如圖所示的扇形環面(由扇形![]() 挖去扇形
挖去扇形![]() 后構成的).已知
后構成的).已知![]() ,線段
,線段![]() 與弧
與弧![]() 、弧
、弧![]() 的長度之和為
的長度之和為![]() 米,圓心角為
米,圓心角為![]() 弧度.
弧度.

(1)求![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(2)記銘牌的截面面積為![]() ,試問
,試問![]() 取何值時,
取何值時,![]() 的值最大?并求出最大值.
的值最大?并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某船在海面![]() 處測得燈塔
處測得燈塔![]() 在北偏東
在北偏東![]() 方向,與
方向,與![]() 相距
相距![]() 海里,測得燈塔
海里,測得燈塔![]() 在北偏西
在北偏西![]() 方向,與
方向,與![]() 相距
相距![]() 海里,船由
海里,船由![]() 向正北方向航行到
向正北方向航行到![]() 處,測得燈塔
處,測得燈塔![]() 在南偏西
在南偏西![]() 方向,這時燈塔
方向,這時燈塔![]() 與
與![]() 相距多少海里?
相距多少海里?![]() 在
在![]() 的什么方向?
的什么方向?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是異面直線,則以下四個命題:①存在分別經過直線
是異面直線,則以下四個命題:①存在分別經過直線![]() 和
和![]() 的兩個互相垂直的平面;②存在分別經過直線
的兩個互相垂直的平面;②存在分別經過直線![]() 和
和![]() 的兩個平行平面;③經過直線
的兩個平行平面;③經過直線![]() 有且只有一個平面垂直于直線
有且只有一個平面垂直于直線![]() ;④經過直線
;④經過直線![]() 有且只有一個平面平行于直線
有且只有一個平面平行于直線![]() ,其中正確的個數有( )
,其中正確的個數有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com