
定義在R上的函數f(x)是最小正周期為2的奇函數, 且當x∈(0, 1)時, f (x)=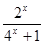 .
.
(1)求f (x)在[-1, 1]上的解析式;
(2)證明f (x)在(—1, 0)上時減函數;
(3)當λ取何值時, 不等式f (x)>λ在R上有解?
(1) f(x)=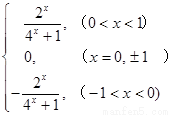 . (2)用定義或導數法均可證明;(3)λ<
. (2)用定義或導數法均可證明;(3)λ<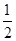
【解析】
試題分析:(1)當x∈(-1, 0)時, - x∈(0,
1).∴由題意可得f(-x)=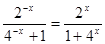 .
.
又f(x)是奇函數,∴f(x)=" -" f (-x) =-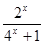 . 2分
. 2分
∵f(-0)= -f(0), ∴f(0)=" 0." 3分
又f(x)是最小正周期為2的函數,∴對任意的x有f(x+2)= f(x).
∴f(-1)=" f(-1+2)=" f(1). 另一面f(-1)="-" f (1), ∴- f(1)=" f(1)" . ∴f(1) = f(-1)=0. 5分
∴f(x)在[-1, 1]上的解析式為 f(x)=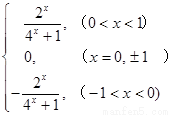 . 6分
. 6分
(2)f (x)在(—1, 0)上時的解析式為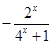 ,∵
,∵ ,∴
,∴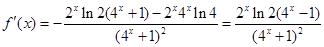 ,又-1<x<0,∴
,又-1<x<0,∴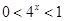 ,∴
,∴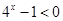 ,∴
,∴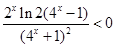 ,∴f (x)在(—1, 0)上時減函數 10分
,∴f (x)在(—1, 0)上時減函數 10分
(3)不等式f(x)>λ在R上有解的λ的取值范圍就是λ小于f(x)在R上的最大值.…12分
由(2)結論可得,當x∈(-1, 0)時,有-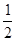 < f(x)= -
< f(x)= -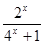 < -
< -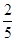 ;
;
又f(x)是奇函數,當x∈(0, 1)時,有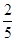 <
f(x)=
<
f(x)=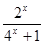 <
<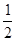 ;
;
∴f(x)在[-1, 1]上的值域是(-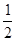 , -
, -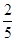 )∪{0}∪(
)∪{0}∪(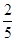 ,
, 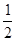 ). 14分
). 14分
由f(x)的周期是2;故f(x)在R上的值域是(-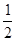 , -
, -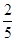 )∪{0}∪(
)∪{0}∪(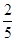 ,
, 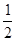 ) 15分
) 15分
∴λ<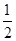 時,不等式f(x)>λ在R上有解. 16分
時,不等式f(x)>λ在R上有解. 16分
考點:本題考查了函數的性質
點評:利用奇偶性求函數解析式問題要注意:(1)在哪個區間求解析式,就設在哪個區間里;(2)轉化為已知的解析式進行代入;(3)利用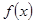 的奇偶性把
的奇偶性把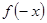 寫成
寫成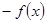 或
或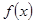 ,從而求出
,從而求出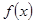 .
.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 2 |
| π |
| 3 |
| x0 |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
已知定義在R上的函數f(x)的圖象是連續不斷的,且有如下對應值表:
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com