
(本題滿分14分)已知圓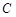 :
: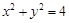 .
.
(Ⅰ)直線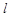 過點
過點 ,且與圓
,且與圓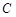 交于
交于 、
、 兩點,若
兩點,若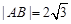 ,求直線
,求直線 的方程;
的方程;
(Ⅱ)過圓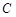 上一動點
上一動點 作平行于
作平行于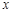 軸的直線
軸的直線 ,設
,設 與
與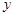 軸的交點為
軸的交點為 ,若向量
,若向量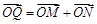 ,求動點
,求動點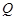 的軌跡方程,并說明此軌跡是什么曲線.
的軌跡方程,并說明此軌跡是什么曲線.
(Ⅰ)x=1,3x-4y+5=0,;(Ⅱ)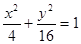 (y≠0)軌跡為長軸長為8,短軸長為4,焦距為4
(y≠0)軌跡為長軸長為8,短軸長為4,焦距為4 且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點
且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點
解析試題分析:(Ⅰ)由直線與圓位置關系得:半徑,半弦長,圓心到直線距離構成勾股,即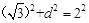 ,因此d=1,又直線
,因此d=1,又直線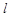 過點
過點 ,故利用直線方程點斜式求解,注意先討論斜率不存在情況:若
,故利用直線方程點斜式求解,注意先討論斜率不存在情況:若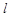 ⊥x軸,直線方程為x=1,A(1,-
⊥x軸,直線方程為x=1,A(1,- ),B(1,
),B(1, ),
),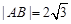 ,適合;若
,適合;若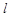 的斜率存在,設
的斜率存在,設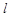 的方程為y=k(x-1)+2,圓心到直線的距離為d=1=
的方程為y=k(x-1)+2,圓心到直線的距離為d=1=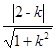 解得k=
解得k=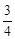 ,直線方程為3x-4y+5=0,(Ⅱ)相關點法求軌跡方程:先找出所求的與已知動點之間關系,代入已知動點軌跡,化簡即得所求動點軌跡方程:設M(
,直線方程為3x-4y+5=0,(Ⅱ)相關點法求軌跡方程:先找出所求的與已知動點之間關系,代入已知動點軌跡,化簡即得所求動點軌跡方程:設M(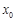 ,
,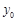 )(
)(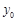 ≠0).則N(0,
≠0).則N(0,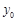 ),Q(x,y),則
),Q(x,y),則 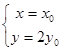 ,又
,又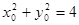 ,動點Q的軌跡方程為
,動點Q的軌跡方程為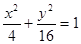 (y≠0)軌跡為長軸長為8,短軸長為4,焦距為4
(y≠0)軌跡為長軸長為8,短軸長為4,焦距為4 且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點
且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點
試題解析:解:(Ⅰ)若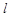 ⊥x軸,直線方程為x=1,A(1,-
⊥x軸,直線方程為x=1,A(1,- ),B(1,
),B(1, ),
),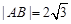 ,適合---3分
,適合---3分
若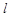 的斜率存在,設
的斜率存在,設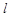 的方程為y=k(x-1)+2,圓心到直線的距離為d=
的方程為y=k(x-1)+2,圓心到直線的距離為d=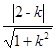 ,圓半徑為2,故
,圓半徑為2,故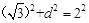 ,k=
,k=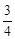 ,直線方程為3x-4y+5="0,"
,直線方程為3x-4y+5="0,"
綜上所求直線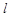 的方程為x=1,3x-4y+5=0,;
的方程為x=1,3x-4y+5=0,;
(Ⅱ)設M(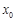 ,
,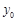 )(
)(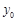 ≠0).則N(0,
≠0).則N(0,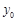 ),Q(x,y),則
),Q(x,y),則 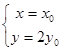
又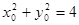 ,動點Q的軌跡方程為
,動點Q的軌跡方程為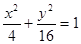 (y≠0)
(y≠0)
軌跡為長軸長為8,短軸長為4,焦距為4 且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點.----6分
且焦點在y軸上的橢圓且去掉橢圓短軸的兩個端點.----6分
考點:直線與圓位置關系,軌跡方程


科目:高中數學 來源: 題型:單選題
已知雙曲線 (a>0,b>0)的右焦點為F(2,0),設A,B為雙曲線上關于原點對稱的兩點,AF的中點為M,BF的中點為N,若原點O在以線段MN為直徑的圓上,若直線AB斜率為
(a>0,b>0)的右焦點為F(2,0),設A,B為雙曲線上關于原點對稱的兩點,AF的中點為M,BF的中點為N,若原點O在以線段MN為直徑的圓上,若直線AB斜率為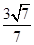 ,則雙曲線的離心率為( )
,則雙曲線的離心率為( )
A. | B. | C.2 | D.4 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
具有線性相關關系的變量x,y ,滿足一組數據如右表所示.若 與
與 的回歸直線方程為
的回歸直線方程為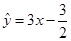 ,則m的值是( )
,則m的值是( )
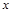 | 0 | 1 | 2 | 3 |
 | -1 | 1 | m | 8 |
 C. 5 D. 6
C. 5 D. 6查看答案和解析>>
科目:高中數學 來源: 題型:單選題
對兩個變量 和
和 進行回歸分析,得到一組樣本數據:
進行回歸分析,得到一組樣本數據: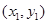 ,
,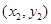 ,…,
,…, ,則下列說法中不正確的是( )
,則下列說法中不正確的是( )
A.由樣本數據得到的回歸方程 必過樣本中心 必過樣本中心 |
| B.殘差平方和越小的模型,擬合的效果越好 |
| C.用相關指數R2來刻畫回歸效果,R2越小,說明模型的擬合效果越好 |
D.若變量 和 和 之間的相關系數為 之間的相關系數為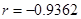 ,則變量 ,則變量 和 和 之間具有線性相關關系 之間具有線性相關關系 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
已知高一年級有學生450人,高二年級有學生750人,高三年級有學生600人.用分層抽樣從該校的這三個年級中抽取一個容量為 的樣本,且每個學生被抽到的概率為0.02,則應從高二年級抽取的學生人數為 .
的樣本,且每個學生被抽到的概率為0.02,則應從高二年級抽取的學生人數為 .
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)某幼兒園有教師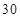 人,對他們進行年齡狀況和受教育程度的調查,其結果如下:
人,對他們進行年齡狀況和受教育程度的調查,其結果如下:
| | 本科 | 研究生 | 合計 |
| 35歲以下 | 5 | 2 | 7 |
| 35~50歲(含35歲和50歲) | 17 | 3 | 20 |
| 50歲以上 | 2 | 1 | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com