
 .
.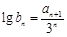 ,試問是否存在正整數p,q(其中1<p<q),使b1,bp,bq成等比數列?若存在,求出所有滿足條件的數組(p,q);若不存在,說明理由.
,試問是否存在正整數p,q(其中1<p<q),使b1,bp,bq成等比數列?若存在,求出所有滿足條件的數組(p,q);若不存在,說明理由.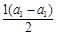 ="0," a3=2
="0," a3=2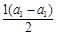 =0. 2分; a3=2; 3分
=0. 2分; a3=2; 3分 ,即
,即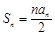 , ① 得
, ① 得 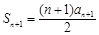 . ②
. ②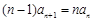 . ③ 5分
. ③ 5分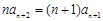 . ④
. ④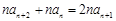 ,即
,即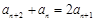 . 7分
. 7分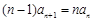 . ③ 5分
. ③ 5分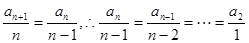 7分
7分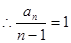 所以,an=n-1. 9分
所以,an=n-1. 9分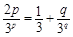 . 11分
. 11分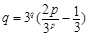 (☆).易知(p,q)=(2,3)為方程(☆)的一組解. 12分
(☆).易知(p,q)=(2,3)為方程(☆)的一組解. 12分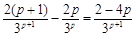 <0,
<0,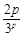 }(p≥3)為遞減數列 14分
}(p≥3)為遞減數列 14分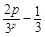 ≤
≤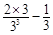 <0,所以此時方程(☆)無正整數解. 15分
<0,所以此時方程(☆)無正整數解. 15分

科目:高中數學 來源:不詳 題型:單選題
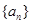 為等差數列,其公差為-2,且a7是a3與a9的等比中項,Sn為
為等差數列,其公差為-2,且a7是a3與a9的等比中項,Sn為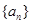 的前n項和(
的前n項和(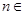 N*),則S10的值為 ( )
N*),則S10的值為 ( )| A.-110 | B.-90 | C.90 | D.110 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com