解:(1)當(dāng)n>1時(shí),b
n=B
n-B
n-1=

-
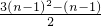
=3n-2
令n=1得b1=1,
∴bn=3n-2.(5分)
(2)由an=(1+

)a
n-1,得
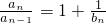
∴an=
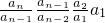
由a
1=2,bn=3n-2知,
an=(1+

)(1+
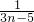
)(1+

)2
=(1+1)(1+

)(1+

)
又
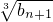
=
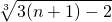
=
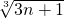
,(5分)
設(shè)c
n=
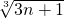
,
當(dāng)n=1時(shí),有(1+1)=
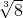
>
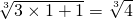
當(dāng)n=2時(shí),有an=(1+1)(1+

)=

=
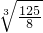
>
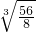
=
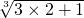
=c
n假設(shè)n=k(k≥1)時(shí)an>c
n成立,
即(1+1)(1+

)(1+
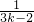
)>
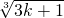
成立,
則n=k+1時(shí),
左邊═(1+1)(1+

)(1+
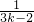
)(1+
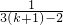
)
>
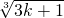
(1+
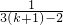
)=
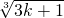
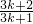
(3分)
右邊=c
k+1=
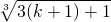
=
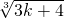
由(ak+1)
3-(c
k+1)
3=(3k+1)
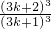
-(3k+4)
=
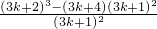
=
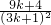
>0,得ak+1>c
k+1成立.
綜合上述,an>c
n對(duì)任何正整數(shù)n都成立.(3分)
分析:(1)由b
n=B
n-B
n-1=

-
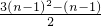
=3n-2,能得到數(shù)列{b
n}的通項(xiàng)公式.
(2)由an=(1+

)a
n-1,得
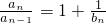
,an=
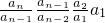
,由a
1=2,bn=3n-2知,an=(1+

)(1+
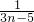
)(1+

)2=(1+1)(1+

)(1+

),由此入手,利用數(shù)學(xué)歸納法能夠證明an>
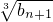
.
點(diǎn)評(píng):本題考查數(shù)列的性質(zhì)和應(yīng)用,解題時(shí)要注意數(shù)列遞推公式的合理運(yùn)用,合理地運(yùn)用數(shù)學(xué)歸納法進(jìn)行證明.

 .
. ) an-1,且a1=2,試比較an與
) an-1,且a1=2,試比較an與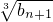 的大小,并證明你的結(jié)論.
的大小,并證明你的結(jié)論. -
-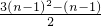 =3n-2
=3n-2 )an-1,得
)an-1,得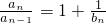
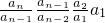
 )(1+
)(1+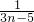 )(1+
)(1+ )2
)2 )(1+
)(1+ )
)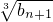 =
=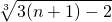 =
=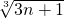 ,(5分)
,(5分)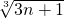 ,
,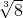 >
>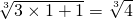
 )=
)=
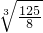 >
>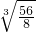 =
=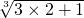 =cn
=cn )(1+
)(1+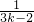 )>
)>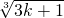 成立,
成立, )(1+
)(1+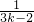 )(1+
)(1+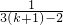 )
)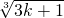 (1+
(1+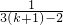 )=
)=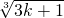
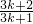 (3分)
(3分)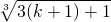 =
=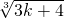
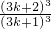 -(3k+4)
-(3k+4)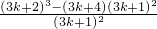
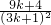 >0,得ak+1>ck+1成立.
>0,得ak+1>ck+1成立. -
-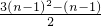 =3n-2,能得到數(shù)列{bn}的通項(xiàng)公式.
=3n-2,能得到數(shù)列{bn}的通項(xiàng)公式. )an-1,得
)an-1,得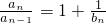 ,an=
,an=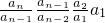 ,由a1=2,bn=3n-2知,an=(1+
,由a1=2,bn=3n-2知,an=(1+ )(1+
)(1+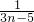 )(1+
)(1+ )2=(1+1)(1+
)2=(1+1)(1+ )(1+
)(1+ ),由此入手,利用數(shù)學(xué)歸納法能夠證明an>
),由此入手,利用數(shù)學(xué)歸納法能夠證明an>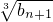 .
.

 名校課堂系列答案
名校課堂系列答案