
【題目】已知正四棱錐的底面邊長是2,側棱長是![]() ,則該正四棱錐的全面積為_____.
,則該正四棱錐的全面積為_____.
【答案】12
【解析】
根據正四棱錐的特點,可知側面是全等的等腰三角形,求出斜高可得側面積,結合底面積可得全面積.
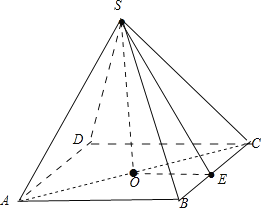
如圖在正四棱錐S﹣ABCD中,O為底面正方形的中心,E為BC的中點,連接OE,SO,SE,
則SO⊥平面ABCD,又BC平面ABCD,所以BC⊥SO,
在三角形ABC中,O,E分別為AC,BC的中點,所以OE∥AB,又因為AB⊥BC,所以BC⊥OE.
又OE∩SO=O,所以BC⊥平面SOE,因為SE平面SOE,
所以SE⊥BC,即SE為側面SBC的斜高,
三角形SBE為直角三角形,所以SE=![]() =2.
=2.
所以該正四棱錐的全面積S全=SABCD+4×SSBC=2×2+4×![]() =4+8=12.
=4+8=12.
故答案為:12.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:
【題目】橢圓的中心在原點,焦點在坐標軸上,焦距為2![]() .一雙曲線和該橢圓有公共焦點,且雙曲線的實半軸長比橢圓的長半軸長小4,雙曲線離心率與橢圓離心率之比為7∶3,求橢圓和雙曲線的方程.
.一雙曲線和該橢圓有公共焦點,且雙曲線的實半軸長比橢圓的長半軸長小4,雙曲線離心率與橢圓離心率之比為7∶3,求橢圓和雙曲線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點.研究表明:“活水圍網”養魚時,某種魚在一定的條件下,每尾魚的平均生長速度![]() (單位:千克/年)是養殖密度
(單位:千克/年)是養殖密度![]() (單位:尾/立方米)的函數.當
(單位:尾/立方米)的函數.當![]() 時,
時,![]() 的值為2千克/年;當
的值為2千克/年;當![]() 時,
時,![]() 是
是![]() 的一次函數;當
的一次函數;當![]() 時,因缺氧等原因,
時,因缺氧等原因,![]() 的值為0千克/年.
的值為0千克/年.
(1)當![]() 時,求
時,求![]() 關于
關于![]() 的函數表達式.
的函數表達式.
(2)當養殖密度![]() 為多少時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
為多少時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖像關于直線
的圖像關于直線![]() 對稱,且
對稱,且![]() .
.
(1)求![]() 的表達式;
的表達式;
(2)若將![]() 圖像上各點的橫坐標變為原來的
圖像上各點的橫坐標變為原來的![]() ,再將所得圖像向右平移
,再將所得圖像向右平移![]() 個單位,得到
個單位,得到![]() 的圖像,且關于
的圖像,且關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有且只有一個實數解,求實數
上有且只有一個實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第二屆中國國際進口博覽會于2019年11月5日至10日在上海國家會展中心舉行,來自151個國家和地區的3617家企業參展,規模和品質均超過首屆.更多新產品、新技術、新服務“全球首發,中國首展”,專(業)精(品)尖(端)特(色)產品精華薈萃.某跨國公司帶來了高端空調模型參展,通過展會調研,中國甲企業計劃在2020年與該跨國公司合資生產此款空調.生產此款空調預計全年需投入固定成本260萬元,每生產x千臺空調,需另投入資金![]() 萬元,且
萬元,且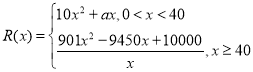 .經測算生產10千臺空調需另投入的資金為4000萬元.由調研知,每臺空調售價為0.9萬元時,當年內生產的空調當年能全部銷售完.
.經測算生產10千臺空調需另投入的資金為4000萬元.由調研知,每臺空調售價為0.9萬元時,當年內生產的空調當年能全部銷售完.
(1)求2020年的企業年利潤![]() (萬元)關于年產量x(千臺)的函數關系式;
(萬元)關于年產量x(千臺)的函數關系式;
(2)2020年產量為多少(千臺)時,企業所獲年利潤最大?最大年利潤是多少?注:利潤=銷售額–成本
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大衍數列,來源于《乾坤譜》中對易傳“大衍之數五十“的推論.主要用于解釋中國傳統文化中的太極衍生原理數列中的每一項,都代表太極衍生過程中,曾經經歷過的兩儀數量總和是中華傳統文化中隱藏著的世界數學史上第一道數列題其規律是:偶數項是序號平方再除以2,奇數項是序號平方減1再除以2,其前10項依次是0,2,4,8,12,18,24,32,40,50,…,如圖所示的程序框圖是為了得到大衍數列的前100項而設計的,那么在兩個判斷框中,可以先后填入( )

A. ![]() 是偶數?,
是偶數?,![]() ? B.
? B. ![]() 是奇數?,
是奇數?,![]() ?
?
C. ![]() 是偶數?,
是偶數?, ![]() ? D.
? D. ![]() 是奇數?,
是奇數?,![]() ?
?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為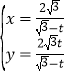 (
(![]() 為參數,且
為參數,且![]() ),以坐標原點為極點,
),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將曲線![]() 的參數方程化為普通方程,并將曲線
的參數方程化為普通方程,并將曲線![]() 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(2)求曲線![]() 與曲線
與曲線![]() 交點的極坐標
交點的極坐標![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com