
| A. | 1 | B. | 2 | C. | 3 | D. | 隨m的變化而變化 |
分析 先求出P的坐標,得出切線方程,求出三角形F1PF2的內切圓的半徑、直線F1M的方程,聯立求出N的橫坐標,即可得出結論.
解答 解:聯立兩曲線方程,消去y可得x=$\frac{2}{\sqrt{m}}$,
設P(x0,y0),直線l的方程為$\frac{{x}_{0}x}{4}+\frac{{y}_{0}y}{4-m}$=1①,
設三角形F1PF2的內切圓的半徑為r,則由等面積可得$2\sqrt{m}{y}_{0}$=(4+$2\sqrt{m}$)r,
∴r=$\frac{\sqrt{m}{y}_{0}}{2+\sqrt{m}}$=yM②,
直線F1M的方程為y=$\frac{{y}_{M}}{1+\sqrt{m}}$(x+$\sqrt{m}$)③,
聯立①②③,化簡可得$3\sqrt{m}$x=6$\sqrt{m}$,
∴xN=2,
∵xM=1,
∴xM+xN=3
故選:C.
點評 本題考查題意、雙曲線方程的性質,考查直線與橢圓的位置關系,正確計算是關鍵.


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | 10 | B. | 7 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
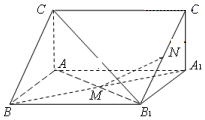 如圖,直三棱柱ABC-A1B1C1中,M,N分別為A1B,B1C1的中點
如圖,直三棱柱ABC-A1B1C1中,M,N分別為A1B,B1C1的中點查看答案和解析>>
科目:高中數學 來源: 題型:填空題
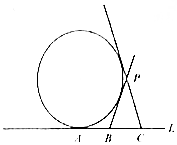 如圖,A,B,C是直線l上的三點,AB=4,BC=4,過A作動圓與直線l相切,過B,C分別做圓的異于l的兩切線,交于點P,則P的軌跡為橢圓.(填軌跡類型,不求方程)
如圖,A,B,C是直線l上的三點,AB=4,BC=4,過A作動圓與直線l相切,過B,C分別做圓的異于l的兩切線,交于點P,則P的軌跡為橢圓.(填軌跡類型,不求方程)查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2\sqrt{2}}{3}$+1 | B. | 2$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$+3 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com