
【題目】如圖,動點![]() 到兩定點
到兩定點![]() 、
、![]() 構成
構成![]() ,且
,且![]() ,設動點
,設動點![]() 的軌跡為
的軌跡為![]() .
.
(1)求軌跡![]() 的方程;
的方程;
(2)設直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與軌跡
,與軌跡![]() 相交于點
相交于點![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.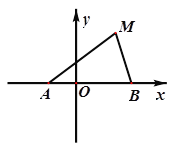
【答案】(1)3x2-y2-3=0(x>1);(2)![]()
【解析】
試題(1)首先由題意可知,顯然![]() ,當
,當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() ,當
,當![]() 時,
時,![]() ,可將
,可將![]() 轉化為正切值即斜率之間的關系,從而可以得到
轉化為正切值即斜率之間的關系,從而可以得到![]() ,
,![]() 所滿足的關系式,即可得到軌跡方程
所滿足的關系式,即可得到軌跡方程![]() :
:![]() ,即
,即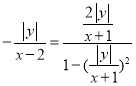 ,化簡可得,
,化簡可得,![]() ,而點
,而點![]() 也在曲線
也在曲線![]() ,軌跡
,軌跡![]() 的方程為
的方程為![]() ;(2)首先將直線方程
;(2)首先將直線方程![]() 與軌跡
與軌跡![]() 的方程
的方程![]() 聯立,消去
聯立,消去![]() 并化簡后可得:
并化簡后可得:![]() ,故若設
,故若設![]() ,
,![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,則問題等價于在
,則問題等價于在![]() 有兩個大于
有兩個大于![]() 的根
的根![]() ,
,![]() ,且
,且![]() 的條件下,求
的條件下,求![]() 的取值范圍,因此首先根據方程
的取值范圍,因此首先根據方程![]() 有兩個大于
有兩個大于![]() 的正根,可求得
的正根,可求得![]() 的取值范圍是
的取值范圍是![]() ,再由求根公式,可將
,再由求根公式,可將![]() 表示為關于
表示為關于![]() 的函數關系:
的函數關系: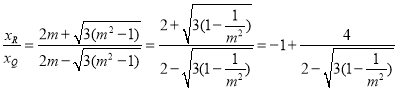 ,在
,在![]() 下,可得
下,可得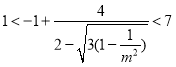 ,即
,即![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:(1)設![]() 的坐標為
的坐標為![]() ,顯然有
,顯然有![]() ,且
,且![]() ,
,
當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() ,
,
當![]() 時,
時,![]() ,由
,由![]() ,
,
有![]() ,即
,即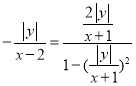 ,化簡可得,
,化簡可得,![]() ,而點
,而點![]() 也在曲線
也在曲線![]() ,
,
綜上可知,軌跡![]() 的方程為
的方程為![]() ;
;
(2)由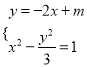 ,消去
,消去![]() 并整理,得
并整理,得![]() ,
,
由題意,方程![]() 有兩根且均在
有兩根且均在![]() 內.設f(x)=x2-4mx+m2+3,
內.設f(x)=x2-4mx+m2+3,
∴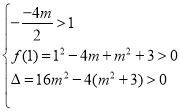 ,解得
,解得![]() ,且
,且![]() ,
,
又∵![]() ,∴
,∴![]() ,設
,設![]() ,
,![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,由
,由![]() 及方程
及方程![]() 有
有
![]() ,
,![]() ,
,
∴ ,
,
由![]() ,得
,得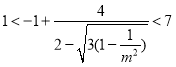 ,
,
故![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】仔細觀察數列給出部分的數字,尋找規律,在空白處填上合適的數字.
(1)2,3,5,8,__________21;(2)8,_______14,17,20,23;
(3)2,4,8,16,_______,64;(4)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,_________.
,_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個直徑為1的小圓沿著直徑為2的大圓內壁的逆時針方向滾動,M和N是小圓的一條固定直徑的兩個端點,那么,當小圓這樣滾過大圓內壁的一周,點M,N在大圓內所繪出的圖形大致是( )
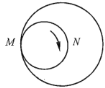
A.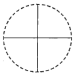 B.
B.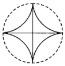 C.
C.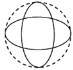 D.
D.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為實現國民經濟新“三步走”的發展戰略目標,國家加大了扶貧攻堅的力度.某地區在2015 年以前的年均脫貧率(脫離貧困的戶數占當年貧困戶總數的比)為![]() .2015年開始,全面實施“精準扶貧”政策后,扶貧效果明顯提高,其中2019年度實施的扶貧項目,各項目參加戶數占比(參加該項目戶數占 2019 年貧困戶總數的比)及該項目的脫貧率見下表:
.2015年開始,全面實施“精準扶貧”政策后,扶貧效果明顯提高,其中2019年度實施的扶貧項目,各項目參加戶數占比(參加該項目戶數占 2019 年貧困戶總數的比)及該項目的脫貧率見下表:
實施項目 | 種植業 | 養殖業 | 工廠就業 | 服務業 |
參加用戶比 |
|
|
|
|
脫貧率 |
|
|
|
|
那么![]() 年的年脫貧率是實施“精準扶貧”政策前的年均脫貧率的( )
年的年脫貧率是實施“精準扶貧”政策前的年均脫貧率的( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a>0,0≤x<2π,若函數y=cos2x-asinx+b的最大值為0,最小值為-4,試求a與b的值,并求使y取得最大值和最小值時的x值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從集市上買回來的蔬菜仍存有殘留農藥,食用時需要清洗數次,統計表中的![]() 表示清洗的次數,
表示清洗的次數,![]() 表示清洗
表示清洗![]() 次后
次后![]() 千克該蔬菜殘留的農藥量(單位:微克).
千克該蔬菜殘留的農藥量(單位:微克).
x | 1 | 2 | 3 | 4 | 5 |
y | 4.5 | 2.2 | 1.4 | 1.3 | 0.6 |
(1)在如圖的坐標系中,描出散點圖,并根據散點圖判斷,![]() 與
與![]() 哪一個適宜作為清洗
哪一個適宜作為清洗![]() 次后
次后![]() 千克該蔬菜殘留的農藥量的回歸方程類型;(給出判斷即可,不必說明理由)
千克該蔬菜殘留的農藥量的回歸方程類型;(給出判斷即可,不必說明理由)

(2)根據判斷及下面表格中的數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
表中![]() ,
,![]() .
.
|
|
|
|
|
| |
3 | 2 | 0.12 | 10 | 0.09 | -8.7 | 0.9 |
(3)對所求的回歸方程進行殘差分析.
附:①線性回歸方程![]() 中系數計算公式分別為
中系數計算公式分別為 ,
,![]() ;
;
② ,
,![]() 說明模擬效果非常好;
說明模擬效果非常好;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
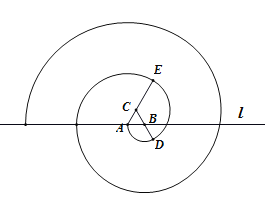
【題目】原始的蚊香出現在宋代.根據宋代冒蘇軾之名編寫的《格物粗談》記載:“端午時,貯浮萍,陰干,加雄黃,作紙纏香,燒之,能祛蚊蟲.”如圖,為某校數學興趣小組用數學軟件制作的“螺旋蚊香”,畫法如下:在水平直線![]() 上取長度為1的線段
上取長度為1的線段![]() ,做一個等邊三角形
,做一個等邊三角形![]() ,然后以點
,然后以點![]() 為圓心,
為圓心,![]() 為半徑逆時針畫圓弧,交線段
為半徑逆時針畫圓弧,交線段![]() 的延長線于點
的延長線于點![]() ,再以點
,再以點![]() 為圓心,
為圓心,![]() 為半徑逆時針畫圓弧,交線段
為半徑逆時針畫圓弧,交線段![]() 的延長線于點
的延長線于點![]() ,以此類推,當得到的“螺旋蚊香”與直線
,以此類推,當得到的“螺旋蚊香”與直線![]() 恰有
恰有![]() 個交點時,“螺旋蚊香”的總長度的最小值為( )
個交點時,“螺旋蚊香”的總長度的最小值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com