
【題目】設n≥2,n∈N* , 有序數組(a1 , a2 , …,an)經m次變換后得到數組(bm , 1 , bm , 2 , …,bm , n),其中b1 , i=ai+ai+1 , bm , i=bm﹣1 , i+bm﹣1 , i+1(i=1,2,…,n),an+1=a1 , bm﹣1 , n+1=bm﹣1 , 1(m≥2).例如:有序數組(1,2,3)經1次變換后得到數組(1+2,2+3,3+1),即(3,5,4);經第2次變換后得到數組(8,9,7).
(1)若ai=i(i=1,2,…,n),求b3 , 5的值;
(2)求證:bm , i= ![]() ai+jCmj , 其中i=1,2,…,n. (注:i+j=kn+t時,k∈N* , i=1,2,…,n,則ai+j=a1)
ai+jCmj , 其中i=1,2,…,n. (注:i+j=kn+t時,k∈N* , i=1,2,…,n,則ai+j=a1)
【答案】
(1)解:依題意(1,2,3,4,5,6,7,8,…,n),
第一次變換為(3,5,7,9,11,13,15,…,n+1),
第二次變換為(8,12,16,20,24,28,…,n+4),
第三次變換為(20,28,36,44,52,…,n+12),
∴b3,5=52
(2)解:用數學歸納法證明:對m∈N*,bm,i= ![]() ai+jCmj,其中i=1,2,…,n,
ai+jCmj,其中i=1,2,…,n,
(i)當m=1時,b1,i= ![]() ai+jC1j,其中i=1,2,…,n,結論成立,
ai+jC1j,其中i=1,2,…,n,結論成立,
(ii)假設m=k時,k∈N*時,bk,i= ![]() ai+jCkj,其中i=1,2,…,n,
ai+jCkj,其中i=1,2,…,n,
則m=k+1時,bk+1,i=bk,i+bk,i+1= ![]() ai+jCkj+
ai+jCkj+ ![]() ai+j+1Ckj=
ai+j+1Ckj= ![]() ai+jCkj+
ai+jCkj+ ![]() ai+j+1Ckj﹣1,
ai+j+1Ckj﹣1,
=aiCk0+ ![]() ai+j(Ckj+Ckj﹣1)+ai+k+1Ckk,
ai+j(Ckj+Ckj﹣1)+ai+k+1Ckk,
=aiCk+10+ ![]() ai+jCk+1j+ai+k+1Ck+1k+1,
ai+jCk+1j+ai+k+1Ck+1k+1,
= ![]() ai+jCk+1j,
ai+jCk+1j,
所以結論對m=k+1時也成立,
由(i)(ii)可知,對m∈N*,bm,i= ![]() ai+jCmj,其中i=1,2,…,n成立
ai+jCmj,其中i=1,2,…,n成立
【解析】(1)根據新定義,分別進行1次,2次,3次變化,即可求出答案,(2)利用數學歸納法證明即可.


科目:高中數學 來源: 題型:
【題目】已知美國蘋果公司生產某款iphone手機的年固定成本為40萬美元,每生產1只還需另投入16美元.設蘋果公司一年內共生產該款iphone手機x萬只并全部銷售完,每萬只的銷售收入為R(x)萬美元,且R(x)= 
(1)寫出年利潤W(萬元)關于年產量x(萬只)的函數解析式;
(2)當年產量為多少萬只時,蘋果公司在該款手機的生產中所獲得的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,點
,點![]() ,直線
,直線![]() .
.
(1)求與圓![]() 相切,且與直線
相切,且與直線![]() 垂直的直線方程;
垂直的直線方程;
(2)在直線![]() 上(
上(![]() 為坐標原點),存在定點
為坐標原點),存在定點![]() (不同于點
(不同于點![]() ),滿足:對于圓
),滿足:對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為一常數,試求所有滿足條件的點
為一常數,試求所有滿足條件的點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:
(1)設所求直線方程為![]() ,利用圓心到直線的距離等于半徑可得關于b的方程,解方程可得
,利用圓心到直線的距離等于半徑可得關于b的方程,解方程可得![]() ,則所求直線方程為
,則所求直線方程為![]()
(2)方法1:假設存在這樣的點![]() ,由題意可得
,由題意可得![]() ,則
,則![]() ,然后證明
,然后證明![]() 為常數
為常數![]() 為即可.
為即可.
方法2:假設存在這樣的點![]() ,使得
,使得![]() 為常數
為常數![]() ,則
,則![]() ,據此得到關于
,據此得到關于![]() 的方程組,求解方程組可得存在點
的方程組,求解方程組可得存在點![]() 對于圓
對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為常數
為常數![]() .
.
試題解析:
(1)設所求直線方程為![]() ,即
,即![]() ,
,
∵直線與圓相切,∴![]() ,得
,得![]() ,
,
∴所求直線方程為![]()
(2)方法1:假設存在這樣的點![]() ,
,
當![]() 為圓
為圓![]() 與
與![]() 軸左交點
軸左交點![]() 時,
時,![]() ;
;
當![]() 為圓
為圓![]() 與
與![]() 軸右交點
軸右交點![]() 時,
時,![]() ,
,
依題意,![]() ,解得,
,解得,![]() (舍去),或
(舍去),或![]() .
.
下面證明點![]() 對于圓
對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為一常數.
為一常數.
設![]() ,則
,則![]() ,
,
∴![]()
![]()
![]() ,
,
從而![]() 為常數.
為常數.
方法2:假設存在這樣的點![]() ,使得
,使得![]() 為常數
為常數![]() ,則
,則![]() ,
,
∴![]() ,將
,將![]() 代入得,
代入得,
![]() ,即
,即
![]() 對
對![]() 恒成立,
恒成立,
∴![]() ,解得
,解得 或
或![]() (舍去),
(舍去),
所以存在點![]() 對于圓
對于圓![]() 上任一點
上任一點![]() ,都有
,都有![]() 為常數
為常數![]() .
.
點睛:求定值問題常見的方法有兩種:
(1)從特殊入手,求出定值,再證明這個值與變量無關.
(2)直接推理、計算,并在計算推理的過程中消去變量,從而得到定值.
【題型】解答題
【結束】
22
【題目】已知函數![]() 的導函數為
的導函數為![]() ,其中
,其中![]() 為常數.
為常數.
(1)當![]() 時,求
時,求![]() 的最大值,并推斷方程
的最大值,并推斷方程![]() 是否有實數解;
是否有實數解;
(2)若![]() 在區間
在區間![]() 上的最大值為-3,求
上的最大值為-3,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知點
中,已知點![]() 為直線
為直線![]() 上一點,過點
上一點,過點![]() 作
作![]() 的垂線與以
的垂線與以![]() 為直徑的圓
為直徑的圓![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
(1)若![]() ,求圓
,求圓![]() 的方程;
的方程;
(2)求證:點![]() 始終在某定圓上.
始終在某定圓上.
(3)是否存在一定點![]() (異于點
(異于點![]() ),使得
),使得![]() 為常數?若存在,求出定點
為常數?若存在,求出定點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某機械廠要將長![]() ,寬
,寬![]() 的長方形鐵皮
的長方形鐵皮![]() 進行裁剪.已知點
進行裁剪.已知點![]() 為
為![]() 的中點,點
的中點,點![]() 在邊
在邊![]() 上,裁剪時先將四邊形
上,裁剪時先將四邊形![]() 沿直線
沿直線![]() 翻折到
翻折到![]() 處(點
處(點![]() 分別落在直線
分別落在直線![]() 下方點
下方點![]() 處,
處,![]() 交邊
交邊![]() 于點
于點![]() ),再沿直線
),再沿直線![]() 裁剪.
裁剪.

(1)當![]() 時,試判斷四邊形
時,試判斷四邊形![]() 的形狀,并求其面積;
的形狀,并求其面積;
(2)若使裁剪得到的四邊形![]() 面積最大,請給出裁剪方案,并說明理由.
面積最大,請給出裁剪方案,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=2x﹣a,g(x)=x+2.
(1)當a=1時,求不等式f(x)+f(﹣x)≤g(x)的解集;
(2)求證: ![]() 中至少有一個不小于
中至少有一個不小于 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() +
+ ![]() =1(a>b>0)的兩個焦點與短軸的一個端點是直角三角形的3個頂點,直線l:y=﹣x+3與橢圓E有且只有一個公共點T.
=1(a>b>0)的兩個焦點與短軸的一個端點是直角三角形的3個頂點,直線l:y=﹣x+3與橢圓E有且只有一個公共點T.
(Ⅰ)求橢圓E的方程及點T的坐標;
(Ⅱ)設O是坐標原點,直線l′平行于OT,與橢圓E交于不同的兩點A、B,且與直線l交于點P.證明:存在常數λ,使得|PT|2=λ|PA||PB|,并求λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為 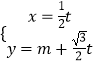 (t為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρ2﹣2ρcosθ﹣4=0
(t為參數),以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρ2﹣2ρcosθ﹣4=0
(1)若直線l與曲線C沒有公共點,求m的取值范圍;
(2)若m=0,求直線l被曲線C截得的弦長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com