
取一根長度為3 m的繩子,拉直后在任意位置剪斷,用隨機模擬法估算剪得兩段的長都不小于1 m的概率有多大?
|
解析:記事件A={剪得兩段的長都不小于1 m}. ①利用計算器或計算機產生一組0到1區間的均勻隨機數a1=RAND. ②經過伸縮變換,a=a1*3. ③統計出試驗總次數N和[1,2]內的隨機數個數N1. ④計算頻率fn(A)=N1/N即為概率P(A)的近似值. 探究:在任意位置剪斷繩子,則剪斷位置到一端點的距離取遍[0,3]內的任意實數,并且每一個實數被取到的可能性相等,因此在任意位置剪斷繩子的所有結果(即基本事件)對應[0,3]上的均勻隨機數,其中[1,2]上的均勻隨機數就表示剪斷位置與端點的距離在[1,2]內,也就是剪得兩段的長都不小于1 m,這樣取得的[1,2]內的隨機數個數與[0,3]內的隨機數個數之比就是事件A發生的頻率. 規律總結:用隨機模擬法估算幾何概率的關鍵是把事件A及基本事件空間對應的區域轉化為隨機數的范圍. |


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源:2014屆廣東省高二第二學期期中考試數學理試卷(解析版) 題型:填空題
取一根長度為3 m的繩子,拉直后在任意位置剪斷,那么剪得兩段的長都不小于1 m的概率是 。
查看答案和解析>>
科目:高中數學 來源:2012年蘇教版高中數學必修3 3.3幾何概型練習卷(二)(解析版) 題型:選擇題
取一根長度為3 m的繩子,拉直后在任意位置剪斷,那么剪得兩段的長都不小于1 m的概率是.
A.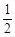 B.
B.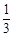 C.
C.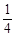 D.不確定
D.不確定
查看答案和解析>>
科目:高中數學 來源:陜西省2009-2010學年度高二第二學期期末考試數學試題(理科) 題型:選擇題
取一根長度為3 m的繩子,拉直后在任意位置剪斷,那么剪得兩段的長都不小于1 m的概率是( )
A.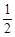 B.
B.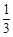 C.
C.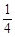 D.不確定
D.不確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com