
分析:在任意位置剪斷繩子,則剪斷位置到一端點的距離取遍[0,3]內的任意數,并且每一個實數被取到都是等可能的.因此在任意位置剪斷繩子的所有結果(基本事件)對應[0,3]上的均勻隨機數,其中取得的[1,2]內的隨機數就表示剪斷位置與端點距離在[1,2]內,也就是剪得兩段長都不小于1 m.這樣取得的[1,2]內的隨機數個數與[0,3]內的個數之比就是事件A發生的概率.
解法一:(1)利用計算器或計算機產生一組0到1區間的均勻隨機數a1=RAND.
(2)經過伸縮變換,a=a1×3.
(3)統計出[1,2]內隨機數的個數N1和[0,3]內隨機數的個數N.
(4)計算頻率fn(A)=![]() 即為概率P(A)的近似值.
即為概率P(A)的近似值.
解法二:做一個帶有指針的圓盤,把圓周三等分,標上刻度[0,3](這里3和0重合).轉動圓盤記下指針在[1,2](表示剪斷繩子位置在[1,2]范圍內)的次數N1及試驗總次數N,則fn(A)即為概率P(A)的近似值.
點評:用隨機數模擬的關鍵是把實際問題中事件A及基本事件總體對應的區域轉化為隨機數的范圍.解法2用轉盤產生隨機數,這種方法可以親自動手操作,但費時費力,試驗次數不可能很大;解法1用計算機產生隨機數,可以產生大量的隨機數,又可以自動統計試驗的結果,同時可以在短時間內多次重復試驗,可以對試驗結果的隨機性和規律性有更深刻的認識.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導學與測試系列答案
導學與測試系列答案科目:高中數學 來源:2014屆廣東省高二第二學期期中考試數學理試卷(解析版) 題型:填空題
取一根長度為3 m的繩子,拉直后在任意位置剪斷,那么剪得兩段的長都不小于1 m的概率是 。
查看答案和解析>>
科目:高中數學 來源:2012年蘇教版高中數學必修3 3.3幾何概型練習卷(二)(解析版) 題型:選擇題
取一根長度為3 m的繩子,拉直后在任意位置剪斷,那么剪得兩段的長都不小于1 m的概率是.
A.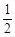 B.
B.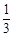 C.
C.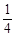 D.不確定
D.不確定
查看答案和解析>>
科目:高中數學 來源:陜西省2009-2010學年度高二第二學期期末考試數學試題(理科) 題型:選擇題
取一根長度為3 m的繩子,拉直后在任意位置剪斷,那么剪得兩段的長都不小于1 m的概率是( )
A.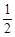 B.
B.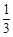 C.
C.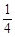 D.不確定
D.不確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com