
【題目】某工廠生產甲、乙兩種產品所得的利潤分別為![]() 和
和![]() (萬元),事先根據相關資料得出它們與投入資金
(萬元),事先根據相關資料得出它們與投入資金![]() (萬元)的數據分別如下表和圖所示:其中已知甲的利潤模型為
(萬元)的數據分別如下表和圖所示:其中已知甲的利潤模型為![]() ,乙的利潤模型為
,乙的利潤模型為![]() .(
.(![]() 為參數,且
為參數,且![]() ).
).
|
|
|
|
|
|
|
|
|
|
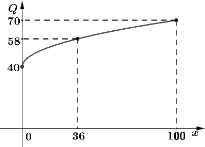
(1)請根據下表與圖中數據,分別求出甲、乙兩種產品所得的利潤與投入資金![]() (萬元)的函數模型
(萬元)的函數模型
(2)今將![]() 萬資金投入生產甲、乙兩種產品,并要求對甲、乙兩種產品的投入資金都不低于
萬資金投入生產甲、乙兩種產品,并要求對甲、乙兩種產品的投入資金都不低于![]() 萬元.設對乙種產品投入資金
萬元.設對乙種產品投入資金![]() (萬元),并設總利潤為
(萬元),并設總利潤為![]() (萬元),如何分配投入資金,才能使總利潤最大?并求出最大總利潤.
(萬元),如何分配投入資金,才能使總利潤最大?并求出最大總利潤.
【答案】(1)![]() ;
;![]() (2)當甲產品投入
(2)當甲產品投入![]() 萬元,乙產品投入
萬元,乙產品投入![]() 萬元時,總利潤最大為
萬元時,總利潤最大為![]() 萬元
萬元
【解析】
(1)根據題意,將數據分別代入甲、乙兩種產品所得的利潤與投入資金![]() (萬元)的函數模型中,解方程組,即可求出函數表達式.
(萬元)的函數模型中,解方程組,即可求出函數表達式.
(2)根據題意,設對乙種產品投資![]() ,對甲種產品投資
,對甲種產品投資![]() ,代入兩個利潤公式,利用換元法求出函數的值域,然后求最大值即可.
,代入兩個利潤公式,利用換元法求出函數的值域,然后求最大值即可.
解:(1)由甲的數據表結合模型![]() 代入兩點可得
代入兩點可得![]()
![]()
代入有![]()
得![]() ,
,![]()
即![]()
由乙的數據圖結合模型![]() 代入三個點可得
代入三個點可得![]() ,
,![]() ,
,![]() 可得
可得
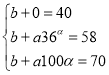 ,
,
得![]() ,
,![]() ,
,![]()
即![]()
(2)根據題意,對乙種產品投資![]() (萬元),對甲種產品投資
(萬元),對甲種產品投資![]() (萬元),
(萬元),
那么總利潤![]()
![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() ,
,
令![]() ,
,![]() ,故
,故![]() ,
,
則![]()
![]() ,
,
所以當![]() 時,即
時,即![]() 時,
時,![]() ,
,
答:當甲產品投入![]() 萬元,乙產品投入
萬元,乙產品投入![]() 萬元時,總利潤最大為
萬元時,總利潤最大為![]() 萬元
萬元


 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案科目:高中數學 來源: 題型:
【題目】 據觀測統計,某濕地公園某種珍稀鳥類的現有個數約![]() 只,并以平均每年
只,并以平均每年![]() 的速度增加.
的速度增加.
(1)求兩年后這種珍稀鳥類的大約個數;
(2)寫出![]() (珍稀鳥類的個數)關于
(珍稀鳥類的個數)關于![]() (經過的年數)的函數關系式;
(經過的年數)的函數關系式;
(3)約經過多少年以后,這種鳥類的個數達到現有個數的![]() 倍或以上?(結果為整數)(參考數據:
倍或以上?(結果為整數)(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 是
是![]() 的中點,點
的中點,點![]() 沿著路徑
沿著路徑![]() 在正方形邊上運動所經過的路程為
在正方形邊上運動所經過的路程為![]() ,
,![]() 的面積為
的面積為![]() .
.

(1)求![]() 的解析式及定義域;
的解析式及定義域;
(2)求![]() 面積的最大值及此時點
面積的最大值及此時點![]() 位置.
位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知雙曲線![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,
,![]() 是雙曲線右支上的一點,
是雙曲線右支上的一點,![]() 與
與![]() 軸交于點
軸交于點![]() 的內切圓在邊
的內切圓在邊![]() 上的切點為
上的切點為![]() ,若
,若![]() ,則雙曲線的離心率是 ( )
,則雙曲線的離心率是 ( )

A. 2 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數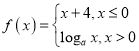 且點
且點![]() 在函數
在函數![]() 的圖象上.
的圖象上.
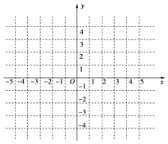
(1)求函數![]() 的解析式,并在圖中的直角坐標系中畫出函數
的解析式,并在圖中的直角坐標系中畫出函數![]() 的圖象;
的圖象;
(2)求不等式![]() 的解集;
的解集;
(3)若方程![]() 有兩個不相等的實數根,求實數
有兩個不相等的實數根,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線x2-![]() =1.
=1.

(1)若一橢圓與該雙曲線共焦點,且有一交點P(2,3),求橢圓方程.
(2)設(1)中橢圓的左、右頂點分別為A、B,右焦點為F,直線l為橢圓的右準線,N為l上的一動點,且在x軸上方,直線AN與橢圓交于點M.若AM=MN,求∠AMB的余弦值;
(3)設過A、F、N三點的圓與y軸交于P、Q兩點,當線段PQ的中點為(0,9)時,求這個圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 分別是雙曲線
分別是雙曲線![]() 的左頂點、右焦點,過
的左頂點、右焦點,過![]() 的直線
的直線![]() 與
與![]() 的一條漸近線垂直且與另一條漸近線和
的一條漸近線垂直且與另一條漸近線和![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點.若
兩點.若![]() ,則
,則![]() 的離心率是( )
的離心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于x的方程2x2﹣ax﹣2=0的兩根分別為α、β(α<β),函數![]()
(1)證明f(x)在區間(α,β)上是增函數;
(2)當a為何值時,f(x)在區間[α,β]上的最大值與最小值之差最小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com