
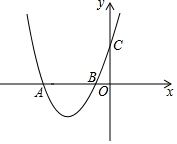
 如圖,拋物線M:y=(x+1)(x+a)(a>1)交x軸于A、B兩點(A在B的左邊),交y軸于C點.拋物線M關于y軸對稱的拋物線N交x軸于P、Q兩點(P在Q的左邊)
如圖,拋物線M:y=(x+1)(x+a)(a>1)交x軸于A、B兩點(A在B的左邊),交y軸于C點.拋物線M關于y軸對稱的拋物線N交x軸于P、Q兩點(P在Q的左邊)分析 (1)令y=0可求得x,則可求得A、B坐標,令x=0可求得C點坐標;
(2)可先求得拋物線N的解析式,則可求得P點坐標,由平行四邊形的性質可知CD=AP,則可求得D點坐標;
(3)由菱形的性質可知AC=AP,則可得到關于a的方程,可求得拋物線N的解析式.
解答 解:
(1)在y=(x+1)(x+a)中,令y=0可得(x+1)(x+a)=0,解得x=-1或x=-a,
∵a>1,
∴-a<-1,
∴A(-a,0),B(-1,0),
令x=0可得y=a,
∴C(0,a),
故答案為:-a,0;0,a;
(2)∵拋物線N與拋物線M關于y軸對稱,
∴拋物線N的解析式為y=(x-1)(x-a),
令y=0可解得x=1或x=a,
∴P(1,0),Q(a,0),
∴AP=1-(-a)=1+a,
∵四邊形ACDP為平行四邊形,
∴CD∥AP,且CD=AP,
∴CD=1+a,且OC=a,
∴D(1+a,a);
(3)∵A(-a,0),C(0,a),
∴AC=$\sqrt{2}$a,
當四邊形ACDP為菱形時則有AP=AC,
∴$\sqrt{2}$a=1+a,解得a=$\sqrt{2}$+1,
∴拋物線N的解析式為y=(x-1)(x-$\sqrt{2}$-1).
點評 本題為二次函數(shù)的綜合應用,涉及函數(shù)圖象與坐標軸的交點、軸對稱、平行四邊形的性質、菱形的性質、勾股定理等知識.在(1)中注意函數(shù)圖象與坐標軸交點的求法,在(2)中由平行四邊形的性質求得AP=CD、AP∥CD是解題的關鍵,在(3)中由菱形的性質得到AC=AP是解題的關鍵.本題考查知識點較多,綜合性較強,難度適中.


科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
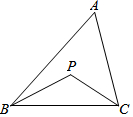 如圖,在△ABC中,BP、CP分別是∠ABC和∠ACB的角平分線.
如圖,在△ABC中,BP、CP分別是∠ABC和∠ACB的角平分線.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com