
若數(shù)列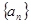 的前
的前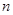 項和
項和 ,則
,則 ________________;
________________;
 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:填空題
對于正項數(shù)列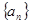 ,定義
,定義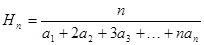 為
為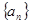 的“蕙蘭”值,現(xiàn)知數(shù)列
的“蕙蘭”值,現(xiàn)知數(shù)列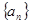 的“蕙蘭”值為
的“蕙蘭”值為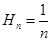 ,則數(shù)列
,則數(shù)列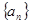 的通項公式為
的通項公式為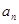 = .
= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
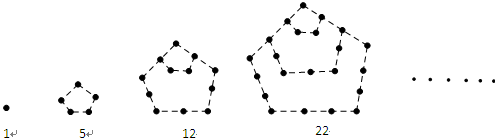
兩千多年前,古希臘畢達哥拉斯學(xué)派的數(shù)學(xué)家曾經(jīng)在沙灘上研究數(shù)學(xué)問題,他們在沙灘上畫點或用小石子來表示數(shù),按照點或小石子能排列的形狀對數(shù)進行分類,如圖2中的實心點個數(shù)1,5,12,22,…,被稱為五角形數(shù),其中第1個五角形數(shù)記作 ,第2個五角形數(shù)記作
,第2個五角形數(shù)記作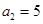 ,第3個五角形數(shù)記作
,第3個五角形數(shù)記作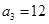 ,第4個五角形數(shù)記作
,第4個五角形數(shù)記作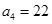 ,…,若按此規(guī)律繼續(xù)下去,得數(shù)列
,…,若按此規(guī)律繼續(xù)下去,得數(shù)列 ,則
,則 ;對
;對 ,
,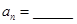 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)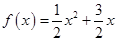 ,數(shù)列
,數(shù)列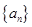 的前
的前 項和為
項和為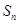 ,點
,點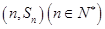 均在函數(shù)
均在函數(shù) 的圖象上.
的圖象上.
(1)求數(shù)列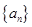 的通項公式
的通項公式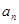 ;
;
(2)令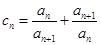 ,證明:
,證明: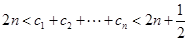 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分14分)已知數(shù)列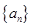 是各項均不為
是各項均不為 的等差數(shù)列,公差為
的等差數(shù)列,公差為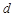 ,
, 為其前
為其前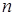 項和,且滿足
項和,且滿足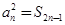 ,
,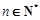 .?dāng)?shù)列
.?dāng)?shù)列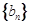 滿足
滿足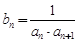 ,
,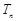 為數(shù)列
為數(shù)列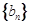 的前
的前 項和.
項和.
(1)求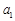 、
、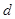 和
和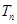 ;
;
(2)若對任意的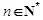 ,不等式
,不等式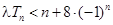 恒成立,求實數(shù)
恒成立,求實數(shù)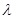 的取值范圍;
的取值范圍;
(3)是否存在正整數(shù)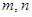
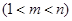 ,使得
,使得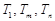 成等比數(shù)列?若存在,求出所有
成等比數(shù)列?若存在,求出所有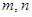 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
在數(shù)列 中,如果存在非零的常數(shù)
中,如果存在非零的常數(shù)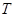 ,使
,使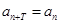 對于任意正整數(shù)
對于任意正整數(shù) 均成立,就稱數(shù)列
均成立,就稱數(shù)列 為周期數(shù)列,其中
為周期數(shù)列,其中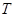 叫做數(shù)列
叫做數(shù)列 的周期. 已知數(shù)列
的周期. 已知數(shù)列 滿足
滿足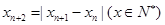 ,若
,若 ,當(dāng)數(shù)列
,當(dāng)數(shù)列 的周期為
的周期為 時,則數(shù)列
時,則數(shù)列 的前2012項的和為
的前2012項的和為
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com