【題目】已知f（x）為定義在R上的奇函數，當x≥0，f（x）=log3（x+3）﹣a，則不等式|f（x）|＜1的解集為 ．
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
cos（2x﹣ 
）．
（1）若sinθ=﹣ 
，θ∈（ 
，2π），求f（θ+ 
）的值；
（2）若x∈[ 
， 
]，求函數f（x）的單調減區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了調查喜愛運動是否和性別有關，我們隨機抽取了50名對象進行了問卷調查得到了如下的2×2列聯表：
喜愛運動 | 不喜愛運動 | 合計 | |
男性 | 5 | ||
女性 | 10 | ||
合計 | 50 |
若在全部50人中隨機抽取2人，抽到喜愛運動和不喜愛運動的男性各一人的概率為 
．
附：
P（K2≥k） | 0.05 | 0.01 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= 
（1）請將上面的2×2列聯表補充完整；
（2）能否在犯錯誤的概率不超過0.001的前提下認為喜愛運動與性別有關？說明你的理由．．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為了了解該校學生對于某項運動的愛好是否與性別有關，通過隨機抽查110名學生，得到如下
的列聯表：
喜歡該項運動 | 不喜歡該項運動 | 總計 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
由公式
，算得
附表：
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
參照附表，以下結論正確的是（ ）
A. 在犯錯誤的概率不超過0.1%的前提下，認為“愛好該項運動與性別有關”
B. 在犯錯語的概率不超過0.1%的前提下，認為“愛好該項運動與性別有關”
C. 有99%以上的把握認為“愛好該項運動與性別無關”
D. 有99%以上的把握認為“愛好該項運動與性別有關”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，連結棱長為2cm的正方體各面的中心得一個多面體容器，從頂點A處向該容器內注水，注滿為止．已知頂點B到水面的高度h以每秒1cm勻速上升，記該容器內水的體積V（cm3）與時間T（S）的函數關系是V（t），則函數V（t）的導函數y=V′（t）的圖象大致是（ ）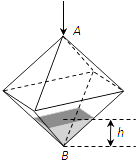 
A.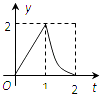
B.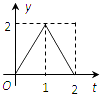
C.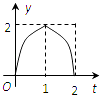
D.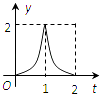
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
