①②
分析:①根據空間四點共面的充要條件若
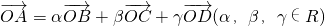
且α+β+γ=1,則A、B、C、D四點在同一平面上;可知①正確;②把
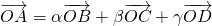
兩邊平方,結合向量數量積的運算即可求得|

|=2故可知②正確;③根據α=a
2,β=a
2009,γ=0,且A、B、C三點共線,可得a
2+a
2009=1,利用等差數列的性質可得a
3+a
2008=1,利用基本不等式即可求得結果;④根據α=

,β=-

,γ=0,得A、B、C三點共線,再算出A分

所成的比λ知④錯.
解答:①若α+β+γ=1,則A、B、C、D四點在同一平面上;①正確;
②

=α

+β

+γ

,兩邊平方結合條件得,

=α
2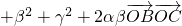
=1+1+1+1=4,
則|

|=2.故②對;
③若α=a
2,β=a
2009,γ=0,且A、B、C三點共線,
∴a
2+a
2009=1,∴a
3+a
2008=1,則
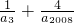
=(
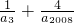
)(a
3+a
2008)≥5+4=9.③錯.
④根據α=

,β=-

,γ=0,得,

=


-


,∴

-

=


-


,
∴

=


,則A、B、C三點共線,
且A分

所成的比λ為-

.故④錯
故答案為①②.
點評:本題主要考查共面向量和共線向量定理以及利用基本不等式求最值等基礎知識和基本方法,要說明一個命題是真命題,必須給出證明,要說明其是假命題,只要舉出反例即可,同時考查了學生靈活應用知識分析解決問題的能力和計算能力.

 、
、 、
、 、
、 滿足:
滿足: =α
=α Z+β
Z+β Z+γ
Z+γ Z(α,β,γ∈R),B、C、D為不共線三點,給出下列命題:
Z(α,β,γ∈R),B、C、D為不共線三點,給出下列命題: ,β=
,β= ,γ=-1,則A、B、C、D四點在同一平面上;
,γ=-1,則A、B、C、D四點在同一平面上; Z|+|
Z|+| |+|
|+| |=1,<
|=1,< ,
, >=<
>=< ,
, >=
>= ,<
,< ,
, >=
>= ,則|
,則| |=2;
|=2;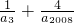 的最小值為10;
的最小值為10; ,β=-
,β=- Z,γ=0,則A、B、C三點共線且A分
Z,γ=0,則A、B、C三點共線且A分 所成的比λ一定為-4
所成的比λ一定為-4 且α+β+γ=1,則A、B、C、D四點在同一平面上;可知①正確;②把
且α+β+γ=1,則A、B、C、D四點在同一平面上;可知①正確;②把 兩邊平方,結合向量數量積的運算即可求得|
兩邊平方,結合向量數量積的運算即可求得| |=2故可知②正確;③根據α=a2,β=a2009,γ=0,且A、B、C三點共線,可得a2+a2009=1,利用等差數列的性質可得a3+a2008=1,利用基本不等式即可求得結果;④根據α=
|=2故可知②正確;③根據α=a2,β=a2009,γ=0,且A、B、C三點共線,可得a2+a2009=1,利用等差數列的性質可得a3+a2008=1,利用基本不等式即可求得結果;④根據α= ,β=-
,β=- ,γ=0,得A、B、C三點共線,再算出A分
,γ=0,得A、B、C三點共線,再算出A分 所成的比λ知④錯.
所成的比λ知④錯. =α
=α +β
+β +γ
+γ ,兩邊平方結合條件得,
,兩邊平方結合條件得, =α2
=α2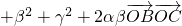 =1+1+1+1=4,
=1+1+1+1=4, |=2.故②對;
|=2.故②對;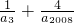 =(
=(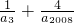 )(a3+a2008)≥5+4=9.③錯.
)(a3+a2008)≥5+4=9.③錯. ,β=-
,β=- ,γ=0,得,
,γ=0,得, =
=
 -
-
 ,∴
,∴ -
- =
=
 -
-
 ,
, =
=
 ,則A、B、C三點共線,
,則A、B、C三點共線, 所成的比λ為-
所成的比λ為- .故④錯
.故④錯

 口算題天天練系列答案
口算題天天練系列答案 、
、 、
、 、
、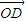 滿足:
滿足: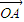 =α
=α Z+β
Z+β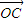 Z+γ
Z+γ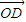 Z(α,β,γ∈R),B、C、D為不共線三點,給出下列命題:
Z(α,β,γ∈R),B、C、D為不共線三點,給出下列命題: ,β=
,β= ,γ=-1,則A、B、C、D四點在同一平面上;
,γ=-1,則A、B、C、D四點在同一平面上; Z|+|
Z|+| |+|
|+| |=1,<
|=1,< ,
, >=<
>=<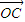 ,
, >=
>= ,<
,<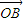 ,
,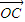 >=
>=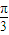 ,則|
,則| |=2;
|=2; 的最小值為10;
的最小值為10; ,β=-
,β=- Z,γ=0,則A、B、C三點共線且A分
Z,γ=0,則A、B、C三點共線且A分 所成的比λ一定為-4
所成的比λ一定為-4