
【題目】已知函數f(x)=(|x|﹣b)2+c,函數g(x)=x+m.
(1)當b=2,m=﹣4時,f(x)≥g(x)恒成立,求實數c的取值范圍;
(2)當c=﹣3,m=﹣2時,方程f(x)=g(x)有四個不同的解,求實數b的取值范圍.
【答案】(1)c≥﹣![]() ;(2)b≥1且1<b<
;(2)b≥1且1<b<![]() .
.
【解析】
試題(1)代入b=2,m=﹣4,![]() ,去絕對值變形為c≥x﹣4﹣(|x|﹣2)2=
,去絕對值變形為c≥x﹣4﹣(|x|﹣2)2=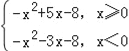 ,只需求得右邊分段函數的最大值.(2)代入c=﹣3,m=﹣2
,只需求得右邊分段函數的最大值.(2)代入c=﹣3,m=﹣2
,得(|x|﹣b)2=x+1有四個不同的解,所以(x﹣b)2=x+1(x≥0)有兩個不同解且
(x+b)2=x+1(x<0)也有兩個不同解,兩個二次函數均在各自區間上有兩個實數解,由根的分布,可解出b的范圍.
試題解析:(1)∵當b=2,m=﹣4時,f(x)≥g(x)恒成立,
∴c≥x﹣4﹣(|x|﹣2)2=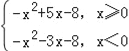 ,由二次函數的性質得c≥﹣
,由二次函數的性質得c≥﹣![]() .
.
(2)(|x|﹣b)2﹣3=x﹣2,即(|x|﹣b)2=x+1有四個不同的解,
∴(x﹣b)2=x+1(x≥0)有兩個不同解以及(x+b)2=x+1(x<0)也有兩個不同解,
由根的分布得b≥1且1<b<![]() ,
,
∴1<b<![]() .
.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:高中數學 來源: 題型:
【題目】![]() 的內切圓與三邊
的內切圓與三邊![]() 的切點分別為
的切點分別為![]() ,已知
,已知![]() ,內切圓圓心
,內切圓圓心![]() ,設點A的軌跡為R.
,設點A的軌跡為R.
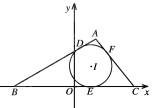
(1)求R的方程;
(2)過點C的動直線m交曲線R于不同的兩點M,N,問在x軸上是否存在一定點Q(Q不與C重合),使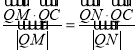 恒成立,若求出Q點的坐標,若不存在,說明理由.
恒成立,若求出Q點的坐標,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,其中a為常數,e是自然對數的底數,
,其中a為常數,e是自然對數的底數,![]() ,曲線
,曲線![]() 在其與y軸的交點處的切線記作
在其與y軸的交點處的切線記作![]() ,曲線
,曲線![]() 在其與x軸的交點處的切線記作
在其與x軸的交點處的切線記作![]() ,且
,且![]() .
.
(1)求![]() 之間的距離;
之間的距離;
(2)對于函數![]() 和
和![]() 的公共定義域中的任意實數
的公共定義域中的任意實數![]() ,稱
,稱![]() 的值為函數
的值為函數![]() 和
和![]() 在
在![]() 處的偏差.求證:函數
處的偏差.求證:函數![]() 和
和![]() 在其公共定義域內的所有偏差都大于2.
在其公共定義域內的所有偏差都大于2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中醫藥,是包括漢族和少數民族醫藥在內的我國各民族醫藥的統稱,是反映中華民族對生命、健康和疾病的認識,具有悠久歷史傳統和獨特理論及技術方法的醫藥學體系,是中華民族的瑰寶.某科研機構研究發現,某品種中醫藥的藥物成分甲的含量![]() (單位:克)與藥物功效
(單位:克)與藥物功效![]() (單位:藥物單位)之間具有關系
(單位:藥物單位)之間具有關系![]() .檢測這種藥品一個批次的5個樣本,得到成分甲的平均值為4克,標準差為
.檢測這種藥品一個批次的5個樣本,得到成分甲的平均值為4克,標準差為![]() 克,則估計這批中醫藥的藥物功效的平均值為( )
克,則估計這批中醫藥的藥物功效的平均值為( )
A.22藥物單位B.20藥物單位C.12藥物單位D.10藥物單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業新研發了一種產品,產品的成本由原料成本及非原料成本組成.每件產品的非原料成本![]() (元)與生產該產品的數量
(元)與生產該產品的數量![]() (千件)有關,經統計得到如下數據:
(千件)有關,經統計得到如下數據:
![]()
根據以上數據,繪制了散點圖.
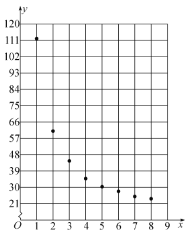
觀察散點圖,兩個變量不具有線性相關關系,現考慮用反比例函數模型![]() 和指數函數模型
和指數函數模型![]() 分別對兩個變量的關系進行擬合.已求得用指數函數模型擬合的回歸方程為
分別對兩個變量的關系進行擬合.已求得用指數函數模型擬合的回歸方程為![]() ,
,![]() 與
與![]() 的相關系數
的相關系數![]() .參考數據(其中
.參考數據(其中![]() ):
):

(1)用反比例函數模型求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)用相關系數判斷上述兩個模型哪一個擬合效果更好(精確到0.01),并用其估計產量為10千件時每件產品的非原料成本;
(3)該企業采取訂單生產模式(根據訂單數量進行生產,即產品全部售出).根據市場調研數據,若該產品單價定為100元,則簽訂9千件訂單的概率為0.8,簽訂10千件訂單的概率為0.2;若單價定為90元,則簽訂10千件訂單的概率為0.3,簽訂11千件訂單的概率為0.7.已知每件產品的原料成本為10元,根據(2)的結果,企業要想獲得更高利潤,產品單價應選擇100元還是90元,請說明理由.
參考公式:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: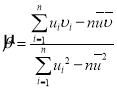 ,
,![]() ,相關系數
,相關系數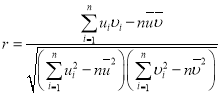 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面為正方形,△PAD為等邊三角形,平面PAD丄平面PCD.
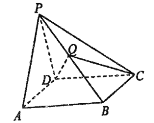
(1)證明:平面PAD丄平面ABCD:
(2)若AB=2,Q為線段的中點,求三棱錐Q-PCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在六棱錐P﹣ABCDEF中,六邊形ABCDEF為正六邊形,平面PAB⊥平面ABCDEF,AB=1,PA![]() ,PB=2.
,PB=2.
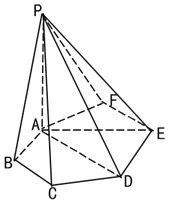
(1)求證:PA⊥平面ABCDEF;
(2)求直線PD與平面PAE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱柱ABCD-A1B1C1D1的底面為菱形,AA1⊥底面ABCD,∠BAD=120°,AB=2,E,F分別為CD,AA1的中點.
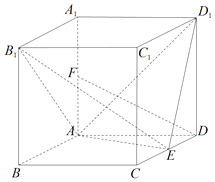
(Ⅰ)求證:DF∥平面B1AE;
(Ⅱ)若直線AD1與平面B1AE所成角的正弦值為![]() ,求AA1的長;
,求AA1的長;
(Ⅲ)在(Ⅱ)的條件下,求二面角B1-AE-D1的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com