
【題目】函數![]() .
.
(1)若函數![]() 的圖象在
的圖象在![]() 處的切線過
處的切線過![]() ,求
,求![]() 的值;
的值;
(2)![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)1;(2)![]() .
.
【解析】
(1)先對函數求導,得到![]() ,根據題意,得到
,根據題意,得到![]() ,推出
,推出![]() ,設
,設![]() ,
,![]() ,對其求導,研究其單調性,求出最小值,即可得出結果;
,對其求導,研究其單調性,求出最小值,即可得出結果;
(2)先由題意,將![]() 在
在![]() 恒成立,轉化為
恒成立,轉化為![]() 在
在![]() 恒成立,設
恒成立,設![]() ,
,![]() ,對其求導,分
,對其求導,分![]() ,
,![]() ,
,![]() 三種情況討論,研究其單調性,得到其大致范圍,即可得出結果.
三種情況討論,研究其單調性,得到其大致范圍,即可得出結果.
(1)因為![]() ,所以
,所以![]() ,
,
由于在![]() 處的切線過
處的切線過![]() ,
,
所以![]() ,即
,即![]() ,
,
化簡得![]() ,即
,即![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() ;
;
從而![]() 在
在![]() 單調遞增,再
單調遞增,再![]() 單調遞減;因此
單調遞減;因此![]() ,
,
所以![]() 有唯一根
有唯一根![]() ;
;
(2)由![]() 得
得![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
因此,![]() 在
在![]() 恒成立,即是
恒成立,即是![]() 在
在![]() 恒成立;
恒成立;
設![]() ,
,![]() ,
,
則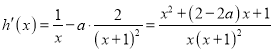 ,
,
當![]() 時,
時,![]() ,此時
,此時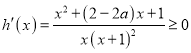 恒成立,
恒成立,
所以![]() 單增,因此
單增,因此![]() ,滿足題意;
,滿足題意;
當![]() 時,
時,![]() 顯然恒成立,此時
顯然恒成立,此時![]() 單增,
單增,
所以![]() ,也滿足題意;
,也滿足題意;
當![]() 時,由
時,由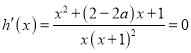 得
得![]() ,
,![]() ,
,
所以方程![]() 必有兩不等實根,不妨設為
必有兩不等實根,不妨設為![]() ,
,
由根與系數關系,![]() ,所以方程
,所以方程![]() 在
在![]() 有唯一根
有唯一根![]() ,
,
即![]() 在
在![]() 有唯一根
有唯一根![]() ,所以易得:
,所以易得:![]() 在
在![]() 單減,
單減,![]() 單增,
單增,
則![]() ,與題意矛盾,不成立;
,與題意矛盾,不成立;
綜上,![]() .
.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:高中數學 來源: 題型:
【題目】若A1,A2,…,Am為集合A={1,2,…,n}(n≥2且n∈N*)的子集,且滿足兩個條件:
①A1∪A2∪…∪Am=A;
②對任意的{x,y}A,至少存在一個i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.則稱集合組A1,A2,…,Am具有性質P.
如圖,作n行m列數表,定義數表中的第k行第l列的數為akl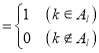 .
.
a11 | a12 | … | a1m |
a21 | a22 | … | a2m |
… | … | … | … |
an1 | an2 | … | anm |
(1)當n=4時,判斷下列兩個集合組是否具有性質P,如果是請畫出所對應的表格,如果不是請說明理由;
集合組1:A1={1,3},A2={2,3},A3={4};
集合組2:A1={2,3,4},A2={2,3},A3={1,4}.
(2)當n=7時,若集合組A1,A2,A3具有性質P,請先畫出所對應的7行3列的一個數表,再依此表格分別寫出集合A1,A2,A3;
(3)當n=100時,集合組A1,A2,…,At是具有性質P且所含集合個數最小的集合組,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的個數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}中,相鄰兩項an,an+1是關于x的方程:x2+3nx+bn![]() 0(n∈N*)的兩實根,且a1=1.
0(n∈N*)的兩實根,且a1=1.
(1)若Sn為數列{an}的前n項和,求S100 ;
(2)求數列{an}和{bn}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(|x|﹣b)2+c,函數g(x)=x+m.
(1)當b=2,m=﹣4時,f(x)≥g(x)恒成立,求實數c的取值范圍;
(2)當c=﹣3,m=﹣2時,方程f(x)=g(x)有四個不同的解,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與x軸的正半軸交于點A,過圓O上任意一點P作x軸的垂線,垂足為Q,線段PQ的中點的軌跡記為曲線
與x軸的正半軸交于點A,過圓O上任意一點P作x軸的垂線,垂足為Q,線段PQ的中點的軌跡記為曲線![]() ,設過原點O且異于兩坐標軸的直線與曲線
,設過原點O且異于兩坐標軸的直線與曲線![]() 交于B,C兩點,直線AB與圓O的另一個交點為M,直線AC與圓O的另一個交點為N,設直線AB,AC的斜率分別為
交于B,C兩點,直線AB與圓O的另一個交點為M,直線AC與圓O的另一個交點為N,設直線AB,AC的斜率分別為![]()
![]() .
.
(1)求![]() 的值;
的值;
(2)判斷![]() 是否為定值?若是,求出此定值;否則,請說明理由.
是否為定值?若是,求出此定值;否則,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若在定義域內存在實數
,若在定義域內存在實數![]() ,滿足
,滿足![]() ,則稱
,則稱![]() 為“局部奇函數”.
為“局部奇函數”.
(1)已知二次函數![]() ,試判斷
,試判斷![]() 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
(2)若![]() 是定義在區間
是定義在區間![]() 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 為定義域
為定義域![]() 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有次水下考古活動中,潛水員需潛入水深為30米的水底進行作業,其用氧量包含以下三個方面:①下潛時,平均速度為每分鐘![]() 米,每分鐘的用氧量為
米,每分鐘的用氧量為![]() 升;②水底作業需要10分鐘,每分鐘的用氧量為0.3升;③返回水面時,速度為每分鐘
升;②水底作業需要10分鐘,每分鐘的用氧量為0.3升;③返回水面時,速度為每分鐘![]() 米,每分鐘用氧量為0.2升;設潛水員在此次考古活動中的總用氧量為
米,每分鐘用氧量為0.2升;設潛水員在此次考古活動中的總用氧量為![]() 升;
升;
(1)將![]() 表示為
表示為![]() 的函數;
的函數;
(2)若![]() ,求總用氧量
,求總用氧量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com