【題目】某校為了鼓勵學生熱心公益，服務社會，成立了“慈善義工社”.2017年12月，該校“慈善義工社”為學生提供了4次參加公益活動的機會，學生可通過網路平臺報名參加活動.為了解學生實際參加這4次活動的情況，該校隨機抽取100名學生進行調查，數據統計如下表，其中“√”表示參加，“×”表示未參加.
（Ⅰ）從該校所有學生中任取一人，試估計其2017年12月恰參加了2次學校組織的公益活動的概率；
（Ⅱ）若在已抽取的100名學生中，2017年12月恰參加了1次活動的學生比4次活動均未參加的學生多17人，求
的值；
（Ⅲ）若學生參加每次公益活動可獲得10個公益積分，試估計該校4000名學生中，2017年12月獲得的公益積分不少于30分的人數.
科目：高中數學 來源： 題型：
【題目】某讀者協會為了了解該地區居民睡前看書的時間情況，從該地區睡前看書的居民中隨機選取了n人進行調查，現將調查結果進行統計得到如圖所示的頻率分布直方圖．則下列說法正確的是( )
A. 睡前看書時間介于40～50分鐘的頻率為0.03
B. 睡前看書時間低于30分鐘的頻率為0.67
C. 若n＝1000，則可估計本次調查中睡前看書時間介于30～50分鐘的有67人
D. 若n＝1000，則可估計本次調查中睡前看書時間介于20～40分鐘的有600人
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f(x)為定義在R上的偶函數，當x≥0時，有f(x＋1)＝－f(x)，且當x∈[0,1)時，f(x)＝log2(x＋1)，給出下列命題
①f(2014)＋f(－2015)＝0；
②函數f(x)在定義域上是周期為2的函數；
③直線y＝x與函數f(x)的圖象有2個交點；
④函數f(x)的值域為(－1,1)．
其中正確的是( )
A. ①② B. ②③
C. ①④ D. ①②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為F,直線
與x軸的交點為P,與拋物線的交點為Q,且
.
(1)求拋物線的方程;
(2)過F的直線l與拋物線相交于A,D兩點,與圓
相交于B,C兩點(A,B兩點相鄰),過A,D兩點分別作拋物線的切線,兩條切線相交于點M,求△ABM與△CDM的面積之積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f(x)是定義域為R的周期函數，最小正周期為2，且
f(1＋x)＝f(1－x)，當－1≤x≤0時，f(x)＝－x.
(1)判斷f(x)的奇偶性；
(2)試求出函數f(x)在區間[－1，2]上的表達式.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校為了鼓勵學生熱心公益，服務社會，成立了“慈善義工社”.2017年12月，該校“慈善義工社”為學生提供了4次參加公益活動的機會，學生可通過網路平臺報名參加活動.為了解學生實際參加這4次活動的情況，該校隨機抽取100名學生進行調查，數據統計如下表，其中“√”表示參加，“×”表示未參加.
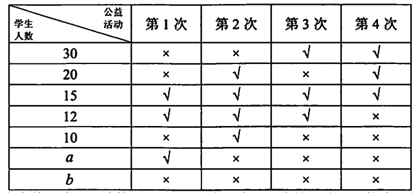
根據表中數據估計，該校4000名學生中約有120名這4次活動均未參加.
（Ⅰ）求
的值；
（Ⅱ）從該校4000名學生中任取一人，試估計其2017年12月恰參加了2次學校組織的公益活動的概率；
（Ⅲ）已知學生每次參加公益活動可獲得10個公益積分，任取該校一名學生，記該生2017年12月獲得的公益積分為
，求隨機變量
的分布列和數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在（0，+∞）上的單調函數f（x），x∈（0，+∞），f[f（x）﹣lnx]=1，則方程f（x）﹣f′（x）=1的解所在區間是 （ ）
A. （2，3） B. 
C. 
D. （1，2）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】共享單車因綠色、環保、健康的出行方式，在國內得到迅速推廣.最近，某機構在某地區隨機采訪了10名男士和10名女士，結果男士、女士中分別有7人、6人表示“經常騎共享單車出行”，其他人表示“較少或不選擇騎共享單車出行”.
（1）從這些男士和女士中各抽取一人，求至少有一人“經常騎共享單車出行”的概率；
（2）從這些男士中抽取一人，女士中抽取兩人，記這三人中“經常騎共享單車出行”的人數為
，求
的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
