已知xy<0,并且4x2-9y2=36.由此能否確定一個函數關系y=f(x),如果能,求出其解析式、定義域和值域;如果不能,請說明理由.
【答案】
分析:根據xy<0得到x、y的正負,然后分兩種情況進一步化簡得到函數的解析式,求出定義域,根據單調性求出函數的值域即可.
解答:解:xy<0?
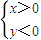
或
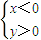
因為4x
2-9y
2=36,故y
2=

所以y=f(x)=
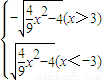
因此能確定一個函數關系y=f(x).其定義域為(-∞,-3)∪(3,+∞).
且不難得到其值域為(-∞,0)∪(0,+∞).
點評:本題主要考查了函數的定義域及其求法,以及函數的表示方法解析式法和函數的值域,屬于基礎題.
