
【題目】設f(x)=asin2x+bcos2x(a,b∈R,ab≠0),若f(x)![]() 對一切x∈R恒成立,給出以下結論:
對一切x∈R恒成立,給出以下結論:
①![]() ;
;
②![]() ;
;
③f(x)的單調遞增區間是![]() ;
;
④函數y=f(x)既不是奇函數也不是偶函數;
⑤存在經過點(a,b)的直線與函數f(x)的圖象不相交,其中正確結論為_____
【答案】①②④
【解析】
先轉化f(x)=asin2x+bcos2x![]() ,根據f(x)
,根據f(x)![]() 對一切x∈R恒成立,得到
對一切x∈R恒成立,得到![]() 是f(x)的最大值或最小值,且f(x)的周期為
是f(x)的最大值或最小值,且f(x)的周期為![]() ,
,
①由![]() 相差四分之一個周期,由相鄰最值點和零點間的關系判斷.②利用軸對稱判斷,是否關于
相差四分之一個周期,由相鄰最值點和零點間的關系判斷.②利用軸對稱判斷,是否關于![]() 對稱.③根據
對稱.③根據![]() 是f(x)的最大值或最小值結合單調性判斷.④由f(x)
是f(x)的最大值或最小值結合單調性判斷.④由f(x)![]() 是奇函數,f(x)
是奇函數,f(x)![]() 是偶函數,判斷.⑤根據三角函數的定義域和值域判斷.
是偶函數,判斷.⑤根據三角函數的定義域和值域判斷.
設f(x)=asin2x+bcos2x![]() ,
,
因為f(x)![]() 對一切x∈R恒成立,
對一切x∈R恒成立,
所以![]() 是f(x)的最大值或最小值.
是f(x)的最大值或最小值.
又因為f(x)的周期為![]() ,
,
①![]() 為四分之一個周期,所以
為四分之一個周期,所以![]() ,故正確.
,故正確.
②因為![]() ,關于
,關于![]() 對稱,所以
對稱,所以![]() ,故正確.
,故正確.
③若![]() 是f(x)的最大值,則
是f(x)的最大值,則![]() ;f(x)的單調遞減區間,故錯誤.
;f(x)的單調遞減區間,故錯誤.
④由![]() ,所以函數不可能轉化為f(x)
,所以函數不可能轉化為f(x)![]() 或f(x)
或f(x)![]() 的形式,所以函數y=f(x)既不是奇函數也不是偶函數,故正確.
的形式,所以函數y=f(x)既不是奇函數也不是偶函數,故正確.
⑤若存在經過點(a,b)的直線與函數f(x)的圖象不相交,則直線與橫軸平行且![]() ,不成立,故錯誤.
,不成立,故錯誤.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,正方形![]() 與梯形
與梯形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上.
上.
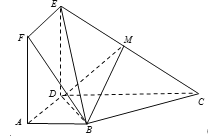
(Ⅰ) 若點![]() 為
為![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(Ⅱ) 求證:平面![]() 平面
平面![]() ;
;
(Ⅲ) 當平面![]() 與平面
與平面![]() 所成二面角的余弦值為
所成二面角的余弦值為![]() 時,求
時,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區有小學21所,中學14所,大學7所,現采取分層抽樣的方法從這些學校中抽取6所學校對學生進行視力調查。
(I)求應從小學、中學、大學中分別抽取的學校數目。
(II)若從抽取的6所學校中隨機抽取2所學校做進一步數據分析,
(1)列出所有可能的抽取結果;
(2)求抽取的2所學校均為小學的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“五一”期間,甲乙兩個商場分別開展促銷活動.
(Ⅰ)甲商場的規則是:凡購物滿100元,可抽獎一次,從裝有大小、形狀相同的4個白球、4個黑球的袋中摸出4個球,中獎情況如下表:
摸出的結果 | 獲得獎金(單位:元) |
4個白球或4個黑球 | 200 |
3個白球1個黑球或3個黑球1個白球 | 20 |
2個黑球2個白球 | 10 |
記![]() 為抽獎一次獲得的獎金,求
為抽獎一次獲得的獎金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商場的規則是:凡購物滿100元,可抽獎10次.其中,第![]() 次抽獎方法是:從編號為
次抽獎方法是:從編號為![]() 的袋中(裝有大小、形狀相同的
的袋中(裝有大小、形狀相同的![]() 個白球和
個白球和![]() 個黑球)摸出
個黑球)摸出![]() 個球,若該次摸出的
個球,若該次摸出的![]() 個球顏色都相同,則可獲得獎金
個球顏色都相同,則可獲得獎金![]() 元;記第
元;記第![]() 次獲獎概率
次獲獎概率![]() .設各次摸獎的結果互不影響,最終所獲得的總獎金為10次獎金之和.
.設各次摸獎的結果互不影響,最終所獲得的總獎金為10次獎金之和.
①求證:![]() ;
;
②若某顧客購買120元的商品,不考慮其它因素,從獲得獎金的期望分析,他應該選擇哪一家商場?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的離心率
的離心率![]() ,拋物線
,拋物線![]() 的焦點恰好是橢圓
的焦點恰好是橢圓![]() 的右焦點
的右焦點![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 作兩條斜率都存在的直線
作兩條斜率都存在的直線![]() ,設
,設![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,
兩點,![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,若
兩點,若![]() 是
是![]() 與
與![]() 的等比中項,求
的等比中項,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,以
,以![]() ,
,![]() 為鄰邊作平行四邊形
為鄰邊作平行四邊形![]() ,連接
,連接![]() 和
和![]() .
.
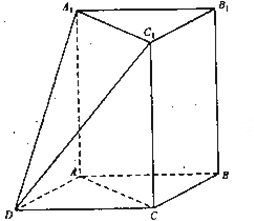
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使平面
,使平面![]() 與平面
與平面![]() 垂直?若存在,求出
垂直?若存在,求出![]() 的長;若不存在,說明理由.
的長;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com