
【題目】已知Sn為數列{an}的前n項和,且有a1=1,Sn+1=an+1(n∈N*).
(1)求數列{an}的通項an;
(2)若bn= ![]() ,求數列{bn}的前n項和Tn;
,求數列{bn}的前n項和Tn;
(3)設ck= ![]() ,{ck}的前n項和為An , 是否存在最小正整數m,使得不等式An<m對任意正整數n恒成立?若存在,求出m的值;若不存在,說明理由.
,{ck}的前n項和為An , 是否存在最小正整數m,使得不等式An<m對任意正整數n恒成立?若存在,求出m的值;若不存在,說明理由.
【答案】
(1)解:當n=1時,a2=S1+1=a1+1=2;
當n≥2時,Sn+1=an+1,Sn﹣1+1=an,相減得an+1=2an,
又a2=2a1,
{an}是首項為1,公比為2的等比數列,
∴ ![]()
(2)解:由(1)知 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
![]() ,
,
兩式相減得 ![]() =
= 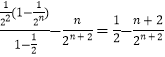 ,
,
∴ ![]()
(3)解:CK= ![]() =
= ![]()
= ![]() .
.
∴ ![]() =
= ![]() =
= ![]() .
.
若不等式∴ ![]() <m對任意正整數n恒成立,則m≥2,
<m對任意正整數n恒成立,則m≥2,
∴存在最小正整數m=2,使不等式∴ ![]() <m對任意正整數n恒成立
<m對任意正整數n恒成立
【解析】(1)在數列遞推式中取n=n﹣1得另一遞推式,作差后即可證得數列為等比數列,代入等比數列的通項公式得答案;(2)把數列{an}的通項代入bn= ![]() ,然后利用錯位相減法求數列{bn}的前n項和Tn;(3)把Sk , Tk代入ck=
,然后利用錯位相減法求數列{bn}的前n項和Tn;(3)把Sk , Tk代入ck= ![]() ,整理后利用裂項相消法化簡,放縮后可證得數列不等式.
,整理后利用裂項相消法化簡,放縮后可證得數列不等式.
【考點精析】掌握數列的前n項和是解答本題的根本,需要知道數列{an}的前n項和sn與通項an的關系 .
.


 優學名師名題系列答案
優學名師名題系列答案科目:高中數學 來源: 題型:
【題目】某公司共有60位員工,為提高員工的業務技術水平,公司擬聘請專業培訓機構進行培訓.培訓的總費用由兩部分組成:一部分是給每位參加員工支付400元的培訓材料費;另一部分是給培訓機構繳納的培訓費.若參加培訓的員工人數不超過30人,則每人收取培訓費1000元;若參加培訓的員工人數超過30人,則每超過1人,人均培訓費減少20元.設公司參加培訓的員工人數為x人,此次培訓的總費用為y元.
(1)求出y與x之間的函數關系式;
(2)請你預算:公司此次培訓的總費用最多需要多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,點
中,點![]() ,直線
,直線![]() ,設圓
,設圓![]() 的半徑為1, 圓心在
的半徑為1, 圓心在![]() 上.
上.

(1)若圓心![]() 也在直線
也在直線![]() 上,過點
上,過點![]() 作圓
作圓![]() 的切線,求切線方程;
的切線,求切線方程;
(2)若圓![]() 上存在點
上存在點![]() ,使
,使![]() ,求圓心
,求圓心![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一種大型商品,A,B兩地都有出售,且價格相同,某地居民從兩地之一購得商品后,運回的費用是:每單位距離A地的運費是B地運費的3倍.已知A,B兩地相距10 km,顧客選A或B地購買這件商品的標準是:包括運費和價格的總費用較低.求A,B兩地的售貨區域的分界線的曲線形狀,并指出曲線上、曲線內、曲線外的居民應如何選擇購貨地點.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b為常數,且a≠0,f(x)=ax2+bx,f(2)=0,方程f(x)=x有兩個相等實數根.
(1)求函數f(x)的解析式;
(2)當x∈[1,2]時,求f(x)的值域;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com