【題目】甲同學(xué)寫出三個不等式：
:
，
:
，
：
，然后將
的值告訴了乙、丙、丁三位同學(xué)，要求他們各用一句話來描述，以下是甲、乙、丙、丁四位同學(xué)的描述：
乙：為整數(shù)；
丙：是成立的充分不必要條件；
丁：是成立的必要不充分條件；
甲：三位同學(xué)說得都對，則的值為__________．
【答案】-1
【解析】
根據(jù)每個同學(xué)的描述得到相應(yīng)的解集，進而推得參數(shù)值.
根據(jù)條件知道，每個同學(xué)說的都是事實，
:
等價于x(x-1)<0,結(jié)合二次函數(shù)的圖像得到，解集為：
；是
成立 的充分不必要條件,故
：
解集為：
是成立的必要不充分條件，故q的解集是r的解集的子集，在
的前提下，結(jié)合二次函數(shù)的性質(zhì)得到，函數(shù)的對稱軸為：
二次函數(shù)和y軸的交點為：
，二次函數(shù)圖像大致如圖：
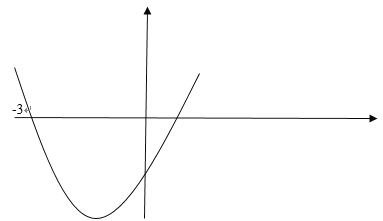
只需要在-3處的函數(shù)值大于0即可，即：
綜上：
，又因為a是整數(shù)，故得到a=-1.
故答案為：-1.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知集合M＝{x|x<－3，或x>5}，P＝{x|(x－a)·(x－8)≤0}．
(1)求M∩P＝{x|5<x≤8}的充要條件；
(2)求實數(shù)a的一個值，使它成為M∩P＝{x|5<x≤8}的一個充分但不必要條件．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知{xn}是各項均為正數(shù)的等比數(shù)列，且x1＋x2＝3，x3－x2＝2.
(1)求數(shù)列{xn}的通項公式；
(2)如圖，在平面直角坐標(biāo)系xOy中，依次連接點P1(x1,1)，P(x2,2)，…，Pn＋1(xn＋1，n＋1)得到折線P1P2…Pn＋1，求由該折線與直線y＝0，x＝x1，x＝xn＋1所圍成的區(qū)域的面積Tn．
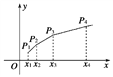
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
（
）的上頂點與拋物線
（
）的焦點
重合.
（1）設(shè)橢圓和拋物線交于
， 
兩點，若
，求橢圓的方程；
（2）設(shè)直線
與拋物線和橢圓均相切，切點分別為
， 
，記
的面積為
，求證： 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)等比數(shù)列
的公比為
，其前
項和為
，前項之積為
，并且滿足條件：
，
，
，下列結(jié)論中正確的是( )
A. 
B. 
C. 
是數(shù)列
中的最大值 D. 數(shù)列無最小值
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知直線
的方程為
，拋物線
：
的焦點為
，點
是拋物線上到直線距離最小的點.
（1）求點的坐標(biāo)；
（2）若直線
與拋物線交于
兩點，
為
中點，且
，求直線的方程.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某市為了改善居民的休閑娛樂活動場所，現(xiàn)有一塊矩形
草坪如下圖所示，已知：
米，
米，擬在這塊草坪內(nèi)鋪設(shè)三條小路
、
和
，要求點
是
的中點，點
在邊
上，點
在邊
時上，且
.
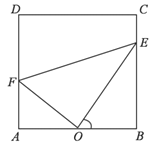
（1）設(shè)
，試求
的周長
關(guān)于
的函數(shù)解析式，并求出此函數(shù)的定義域；
（2）經(jīng)核算，三條路每米鋪設(shè)費用均為
元，試問如何設(shè)計才能使鋪路的總費用最低？并求出最低總費用.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為進一步貫徹落實“十九”大精神，某高校組織了“歌頌祖國，緊跟黨走”為主題的黨史知識競賽,從參加競賽的學(xué)生中，隨機抽取40名學(xué)生，將其成績分為六段
，
，
，得到如圖所示的頻率分布直方圖.
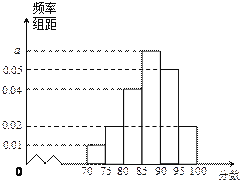
（1）求圖中
的值；
（2）若從競賽成績在
與
兩個分?jǐn)?shù)段的學(xué)生
中隨機選取兩名學(xué)生，設(shè)這兩名學(xué)生的競賽成績之差的絕對值不大于
分為事件,求事件發(fā)生的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）=x3+ex-e-x．
（1）判斷此函數(shù)的奇偶性，并說明理由；
（2）判斷此函數(shù)的單調(diào)性（不需要證明）；
（3）求不等式f（2x-1）+f（-3）＜0的解集．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com