
【題目】已知函數![]() ,且.
,且. ![]()
(1)求函數![]() 的解析式;
的解析式;
(2)若對任意![]() ,都有
,都有![]() ,求的
,求的![]() 取值范圍;
取值范圍;
(3)證明函數![]() 的圖象在
的圖象在![]() 圖象的下方.
圖象的下方.
【答案】(1)![]() (2)
(2)![]() (3)見解析
(3)見解析
【解析】
試題(1)首先求出函數的定義域![]() ,再對
,再對![]() 求導,代入
求導,代入![]() ,解方程可得
,解方程可得![]() ,即可求得函數
,即可求得函數![]() 的解析式;
的解析式;
(2)由題意可得![]() 恒成立,即
恒成立,即![]() 恒成立,令
恒成立,令![]() ,求出
,求出![]() 的導數,單調區間,求得最大值,即可得到
的導數,單調區間,求得最大值,即可得到![]() 的取值范圍;
的取值范圍;
(3)要證明函數![]() 的圖象在
的圖象在![]() 圖象的下方.,即證
圖象的下方.,即證![]() 恒成立,即證
恒成立,即證![]() ,即證
,即證![]() ,令
,令![]() 求得導數,得到單調性,即可得證.
求得導數,得到單調性,即可得證.
試題解析:(1)易知函數的定義域![]()
![]() 所以
所以![]() ,又
,又![]()
![]() ;
;
(2)若對任意的![]() ,都有
,都有![]()
即![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
令![]() ,則
,則![]()
當![]() 時,
時,![]() 所以
所以![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() 所以
所以![]() 單調遞減;
單調遞減;
![]() 時,
時,![]() 有最大值
有最大值![]() ,即
,即![]() 的取值范圍為
的取值范圍為![]()
(3)要證明函數![]() 的圖象在
的圖象在![]() 圖象的下方.,即證
圖象的下方.,即證![]() 恒成立,即
恒成立,即![]()
由(2)可得:![]() ,所以
,所以![]()
要證明![]() ,只要證明
,只要證明![]() ,即證
,即證![]()
令![]() 則
則![]() 當
當![]() 時,
時,![]() 所以
所以![]() 單調遞增,
單調遞增,![]()
即![]()
所以![]() 從而得到
從而得到![]() ,
,
所以函數![]() 的圖象在
的圖象在![]() 圖象的下方
圖象的下方


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:
【題目】如圖,四邊形![]() 中(圖1),
中(圖1),![]() 是
是![]() 的中點,
的中點,![]() ,
,![]()
![]() ,
,![]() 將(圖1)沿直線
將(圖1)沿直線![]() 折起,使二面角
折起,使二面角![]() 為
為![]() (如圖2).
(如圖2).
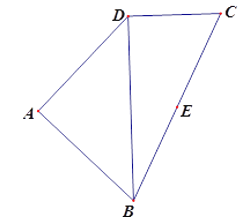
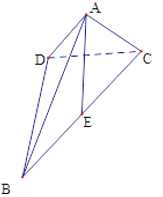
圖1 圖2
(1)求證:![]() 平面
平面![]() ;
;
(2)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 、
、![]() 分別是橢圓
分別是橢圓![]()
![]()
![]() 的左、右焦點,點
的左、右焦點,點![]() 是橢圓
是橢圓![]() 上一點,且
上一點,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() ,其中
,其中![]() 為坐標原點,判斷
為坐標原點,判斷![]() 到直線
到直線![]() 的距離是否為定值?若是,求出該定值;若不是,請說明理由.
的距離是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線的焦點為F,過拋物線上一點P作拋物線的切線交x軸于點D,交y軸于Q點,當時,.
(1)判斷的形狀,并求拋物線的方程;
(2)若兩點在拋物線上,且滿足![]() ,其中點,若拋物線上存在異于
,其中點,若拋物線上存在異于![]() 的點H,使得經過
的點H,使得經過![]() 三點的圓和拋物線在點處有相同的切線,求點H的坐標.
三點的圓和拋物線在點處有相同的切線,求點H的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 的前n項和為
的前n項和為![]() ,
, ![]() ,
, ![]() ,數列
,數列![]() 滿足:
滿足: ![]() ,
, ![]() ,
, ![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]()
(1)求數列![]() 的通項公式及前n項和;
的通項公式及前n項和;
(2)求數列![]() 的通項公式及前n項和;
的通項公式及前n項和;
(3)記集合 ,若M的子集個數為16,求實數
,若M的子集個數為16,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)貴廣高速鐵路自貴陽北站起,經黔南州、黔東南、廣西桂林、賀州、廣東肇慶、佛山終至廣州南站. 其中廣東省內有懷集站、廣寧站、肇慶東站、三水南站、佛山西站、廣州南站共6個站. 記者對廣東省內的6個車站隨機抽取3個進行車站服務滿意度調查.
(1)求抽取的車站中含有佛山市內車站(包括三水南站和佛山西站)的概率;
(2)設抽取的車站中含有肇慶市內車站(包括懷集站、廣寧站、肇慶東站)個數為X,求X的分布列及其均值(即數學期望).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有關于![]() 的一元二次方程
的一元二次方程![]() .
.
(Ⅰ)若![]() 是從
是從![]() 四個數中任取的一個數,
四個數中任取的一個數,![]() 是從
是從![]() 三個數中任取的一個數,求上述方程有實根的概率.
三個數中任取的一個數,求上述方程有實根的概率.
(Ⅱ)若![]() 是從區間
是從區間![]() 任取的一個數,
任取的一個數,![]() 是從區間
是從區間![]() 任取的一個數,求上述方程有實根的概率.
任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學對高三年級進行身高統計,測量隨機抽取的20名學生的身高,其頻率分布直方圖如下(單位:cm)

(1)根據頻率分布直方圖,求出這20名學生身高中位數的估計值和平均數的估計值.
(2)在身高為140—160的學生中任選2個,求至少有一人的身高在150—160之間的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com