
【題目】如圖,長途車站P與地鐵站O的距離為![]() 千米,從地鐵站O出發有兩條道路l1,l2,經測量,l1,l2的夾角為45°,OP與l1的夾角
千米,從地鐵站O出發有兩條道路l1,l2,經測量,l1,l2的夾角為45°,OP與l1的夾角![]() 滿足tan
滿足tan![]() =
=![]() (其中0<θ<
(其中0<θ<![]() ),現要經過P修條直路分別與道路l1,l2交匯于A,B兩點,并在A,B處設立公共自行車停放點.
),現要經過P修條直路分別與道路l1,l2交匯于A,B兩點,并在A,B處設立公共自行車停放點.

(1)已知修建道路PA,PB的單位造價分別為2m元/千米和m元/千米,若兩段道路的總造價相等,求此時點A,B之間的距離;
(2)考慮環境因素,需要對OA,OB段道路進行翻修,OA,OB段的翻修單價分別為n元/千米和![]() n元/千米,要使兩段道路的翻修總價最少,試確定A,B點的位置.
n元/千米,要使兩段道路的翻修總價最少,試確定A,B點的位置.
【答案】(1)![]() (2)要使OA,OB段道路的翻修總價最少,A位于距O點3千米處,B位于距點
(2)要使OA,OB段道路的翻修總價最少,A位于距O點3千米處,B位于距點![]() 千米處.
千米處.
【解析】
(1)以O為原點,直線OA為x軸建立平面直角坐標系,得到![]() 的方程,進而求得點P的坐標,
的方程,進而求得點P的坐標,
法一:由題意得![]() ,求得B點的縱坐標為3,進而得到點
,求得B點的縱坐標為3,進而得到點![]() 的坐標,即可得到答案。
的坐標,即可得到答案。
法二:由題意得2mPA=mPB,求得![]() ,根據向量相等,求得點
,根據向量相等,求得點![]() 的坐標,即可求解。
的坐標,即可求解。
(2)法一:由題意,得到造價的表達式![]() ,設
,設![]() ,得到要使S最小,只要y最小,分類討論,即可求解。
,得到要使S最小,只要y最小,分類討論,即可求解。
法二:作![]() 交OB于M,交y軸于點Q,作
交OB于M,交y軸于點Q,作![]() 交OA于N,求得OQ=1,進而得到總造價
交OA于N,求得OQ=1,進而得到總造價![]() ,設
,設![]() ,要使S最小,只要y最小,即可求解。
,要使S最小,只要y最小,即可求解。
以O為原點,直線OA為x軸建立平面直角坐標系,
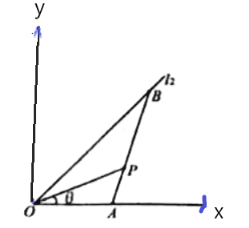
因為![]() ,所以
,所以![]() ,
,
設P(2t,t),由OP=![]() ,得t=1,所以P(2,1)
,得t=1,所以P(2,1)
法一:由題意得![]() ,所以BP=2PA,所以B點的縱坐標為3,
,所以BP=2PA,所以B點的縱坐標為3,
有因為點B在直線![]() 上,所以B(3,3)
上,所以B(3,3)
所以![]() .
.
法二:由題意得2mPA=mPB,所以![]() .
.
設A(a,0)(a>0),又點B在射線y=x(x>0)上,所以可設B(b,b)(b>0),
由![]() ,得
,得![]() 所以
所以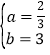
所以![]() .
.
答:A,B之間的距離為![]() 千米.
千米.
(2)法一:設總造價為S.則![]()
設![]() ,要使S最小,只要y最小
,要使S最小,只要y最小
當![]() 軸時,A(2,0),這時OA=2,
軸時,A(2,0),這時OA=2,![]() ,
,
所以![]() .
.
當AB與x軸不垂直時,設直線AB方程為![]() ,
,
令y=0,得點A的橫坐標為![]() ,所以
,所以![]() ,
,
令x=y,得點B的橫坐標為![]() ,
,
因為![]() 且
且![]() ,所以k<0或k>1,
,所以k<0或k>1,
此時![]() ,
,
![]() ,
,
當k<0時,y在![]() 上遞減,在(-1,0)上遞增,
上遞減,在(-1,0)上遞增,
所以![]() ,此時
,此時![]() ;
;
當k>1時,![]()
綜上所述,要使OA,OB段道路的翻修總價最少,A位于距O點3千米處,B位于距點![]() 千米處.
千米處.
法二:如圖,作![]() 交OB于M,交y軸于點Q
交OB于M,交y軸于點Q
作![]() 交OA于N,困為P(2,1),所以OQ=1
交OA于N,困為P(2,1),所以OQ=1
又因為∠BOQ=45°,所以![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,
,
設總造價為S,則![]() ,
,
設![]() ,要使S最小,只要y最小.
,要使S最小,只要y最小.
![]()
當且僅當![]() 時取等號,此時
時取等號,此時![]() .
.
答:要使OA,OB段道路的翻修總價最少,位于距O點3千米處,B位于距O點![]() 千米處.
千米處.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 與曲線
與曲線![]() 公共點的極坐標;
公共點的極坐標;
(2)設過點![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() 的中點為
的中點為![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,“嫦娥一號”探月衛星沿地月轉移軌道飛向月球,在月球附近一點![]() 變軌進入以月球球心
變軌進入以月球球心![]() 為一個焦點的橢圓軌道Ⅰ繞月飛行,之后衛星在
為一個焦點的橢圓軌道Ⅰ繞月飛行,之后衛星在![]() 點第二次變軌進入仍然以
點第二次變軌進入仍然以![]() 為一個焦點的橢圓軌道Ⅱ繞月飛行,最終衛星在
為一個焦點的橢圓軌道Ⅱ繞月飛行,最終衛星在![]() 點第三次變軌進入以
點第三次變軌進入以![]() 為圓心的圓形軌道Ⅲ繞月飛行,若用
為圓心的圓形軌道Ⅲ繞月飛行,若用![]() 和
和![]() 分別表示橢圓軌道Ⅰ和Ⅱ的焦距,用
分別表示橢圓軌道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分別表示橢圓軌道Ⅰ和Ⅱ的長軸的長,給出下列式子:
分別表示橢圓軌道Ⅰ和Ⅱ的長軸的長,給出下列式子:
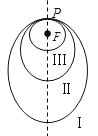
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正確式子的序號是( )
A.①③B.②③C.①④D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某種螺帽是由一個半徑為2的半球體挖去一個正三棱錐構成的幾何體,該正三棱錐的底面三角形內接于半球底面大圓,頂點在半球面上,則被挖去的正三棱錐體積為_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年,國家逐步推行全新的高考制度.新高考不再分文理科.山東省采用3+3模式,其中語文、數學、外語三科為必考科目,每門科目滿分均為150分.另外考生還要依據想考取的高校及專業的要求,結合自己的興趣愛好等因素,在思想政治、歷史、地理、物理、化學、生物6門科目中自選3門參加考試(6選3),每門科目滿分均為100分.為了應對新高考,某高中從高一年級1100名學生(其中男生600人,女生500人)中,采用分層抽樣的方法從中抽取n名學生進行調查,其中女生抽取50人.
(1)求n的值;
(2)學校計劃在高一上學期開設選修中的“物理”和“地理”兩個科目,為了了解學生對這兩個科目的選課情況,對抽取到的n名學生進行問卷調查(假定每名學生在“物理”和“地理”這兩個科目中必須選擇一個科目且只能選擇一個科目).下表是根據調查結果得到的一個不完整的2×2列聯表,請將下面的2×2列聯表補充完整,并判斷是否有99%的把握認為選擇科目與性別有關?說明你的理由;
選擇“物理” | 選擇“地理” | 總計 | |
男生 | 10 | ||
女生 | 30 | ||
合計 |
(3)按(2)中選“物理”的男生女生的比例進行分層抽樣,從選“物理”的學生中抽出8名學生,再從這8名學生中抽取3人組成物理興趣小組,設這3人中女生的人數為X,求X的概率分布列及數學期望.
附![]()
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春節前后,一場突如其來的新冠肺炎疫情在全國蔓延.疫情就是命令,防控就是責任.在黨中央的堅強領導和統一指揮下,全國人民眾志成城、團結一心,掀起了一場堅決打贏疫情防控阻擊戰的人民戰爭.下圖表展示了2月14日至29日全國新冠肺炎疫情變化情況,根據該折線圖,下列結論正確的是( )
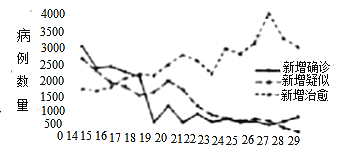
A.16天中每日新增確診病例數量呈下降趨勢且19日的降幅最大
B.16天中每日新增確診病例的中位數小于新增疑似病例的中位數
C.16天中新增確診、新增疑似、新增治愈病例的極差均大于2000
D.19日至29日每日新增治愈病例數量均大于新增確診與新增疑似病例之和
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對![]() 四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
四件參賽作品只評一件一等獎,在評獎揭曉前,甲,乙,丙,丁四位同學對這四件參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”; 乙說:“
作品獲得一等獎”; 乙說:“ ![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“ ![]() 兩件作品未獲得一等獎”; 丁說:“是
兩件作品未獲得一等獎”; 丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
評獎揭曉后,發現這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】心理學家發現視覺和空間能力與性別有關,某數學興趣小組為了驗證這個結論,從興趣小組中按分層抽樣的方法抽取50名同學,給所有同學幾何和代數各一題,讓各位同學自由選擇一道題進行解答,統計情況如下表:(單位:人)
幾何題 | 代數題 | 總計 | |
男 同學 | 22 | 8 | 30 |
女同學 | 8 | 12 | 20 |
總計 | 30 | 20 | 50 |
(1)能否據此判斷有97.5%的把握認為視覺和空間能力與性別有關?
(2)現從選擇幾何題的8名女生中任意抽取兩人對他們的答題進行研究,記甲、乙兩名女生被抽到的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
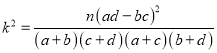
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com