
【題目】設(shè)x,y,z∈R,z(x+2y)=m.
(1)若m=1,求![]() 的最小值;
的最小值;
(2)若x2+2y2+3z2=m2﹣8,求實(shí)數(shù)m的取值范圍.
【答案】(1)1;(2)(﹣∞,﹣4]∪[4,+∞).
【解析】
(1)由均值不等式及其變形,可得到兩數(shù)的平方和不小于兩數(shù)和平方的一半,對![]() 運(yùn)用剛得到的基本不等式的變形性質(zhì),結(jié)合已知進(jìn)行求解即可;
運(yùn)用剛得到的基本不等式的變形性質(zhì),結(jié)合已知進(jìn)行求解即可;
(2)由均值不等式和絕對值不等式得x2+2y2+3z2=(x2+z2)+2(y2+z2)≥2|xz|+4|yz|≥2|xz+2yz|=2|z(x+2y)|=|m|,進(jìn)而得到關(guān)于m的不等式,解出即可.
(1)∵a2+b2≥2ab,
∴2(a2+b2)≥(a+b)2,即a2+b2![]() (a+b)2,
(a+b)2,
∴x2+4y2![]() z2
z2![]() (x+2y)2
(x+2y)2![]() z2
z2![]() 2|(x+2y)z|=1,
2|(x+2y)z|=1,
當(dāng)且僅當(dāng)x=2y,x+2y=z時(shí),即x=2y![]() z,等號成立,
z,等號成立,
∴x2+4y2![]() z2的最小值是1.
z2的最小值是1.
(2)∵m2﹣8=x2+2y2+3z2=(x2+z2)+2(y2+z2)≥2|xz|+4|yz|,(當(dāng)且僅當(dāng)|x|=|y|=|z|時(shí)等號成立),
又2|xz|+4|yz|≥2|xz+2yz|=2|z(x+2y)|=|m|,(當(dāng)且僅當(dāng)xz與yz非異號時(shí)等號成立).
∴m2﹣8≥2|m|,即m2﹣2|m|﹣8≥0,
解得|m|≥4,即m≥4或m≤﹣4,
所以m的取值范圍為(﹣∞,﹣4]∪[4,+∞).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的四個(gè)頂點(diǎn)圍成的菱形的面積為
的四個(gè)頂點(diǎn)圍成的菱形的面積為![]() ,橢圓的一個(gè)焦點(diǎn)為
,橢圓的一個(gè)焦點(diǎn)為![]() .
.
(1)求橢圓的方程;
(2)若![]() ,
,![]() 為橢圓上的兩個(gè)動點(diǎn),直線
為橢圓上的兩個(gè)動點(diǎn),直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() 的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“難度系數(shù)”反映試題的難易程度,難度系數(shù)越大,題目得分率越高,難度也就越小.“難度系數(shù)”的計(jì)算公式為![]() ,其中,
,其中,![]() 為難度系數(shù),
為難度系數(shù),![]() 為樣本平均失分,
為樣本平均失分,![]() 為試卷總分(一般為100分或150分).某校高三年級的李老師命制了某專題共5套測試卷(每套總分150分),用于對該校高三年級480名學(xué)生進(jìn)行每周測試.測試前根據(jù)自己對學(xué)生的了解,預(yù)估了每套試卷的難度系數(shù),如下表所示:
為試卷總分(一般為100分或150分).某校高三年級的李老師命制了某專題共5套測試卷(每套總分150分),用于對該校高三年級480名學(xué)生進(jìn)行每周測試.測試前根據(jù)自己對學(xué)生的了解,預(yù)估了每套試卷的難度系數(shù),如下表所示:
試卷序號 | 1 | 2 | 3 | 4 | 5 |
考前預(yù)估難度系數(shù) | 0.7 | 0.64 | 0.6 | 0.6 | 0.55 |
測試后,隨機(jī)抽取了50名學(xué)生的數(shù)據(jù)進(jìn)行統(tǒng)計(jì),結(jié)果如下:
試卷序號 | 1 | 2 | 3 | 4 | 5 |
實(shí)測平均分 | 102 | 99 | 93 | 93 | 87 |
(1)根據(jù)試卷2的難度系數(shù)估計(jì)這480名學(xué)生第2套試卷的平均分;
(2)從抽樣的50名學(xué)生的5套試卷中隨機(jī)抽取2套試卷,記這2套試卷中平均分超過96分的套數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(3)試卷的預(yù)估難度系數(shù)和實(shí)測難度系數(shù)之間會有偏差.設(shè)![]() 為第
為第![]() 套試卷的實(shí)測難度系數(shù),并定義統(tǒng)計(jì)量
套試卷的實(shí)測難度系數(shù),并定義統(tǒng)計(jì)量![]() ,若
,若![]() ,則認(rèn)為本專題的5套試卷測試的難度系數(shù)預(yù)估合理,否則認(rèn)為不合理.試檢驗(yàn)本專題的5套試卷對難度系數(shù)的預(yù)估是否合理.
,則認(rèn)為本專題的5套試卷測試的難度系數(shù)預(yù)估合理,否則認(rèn)為不合理.試檢驗(yàn)本專題的5套試卷對難度系數(shù)的預(yù)估是否合理.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
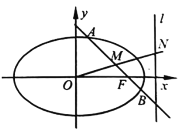
【題目】已知橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,右準(zhǔn)線為
,右準(zhǔn)線為![]() .過點(diǎn)
.過點(diǎn)![]() 作與坐標(biāo)軸都不垂直的直線與橢圓
作與坐標(biāo)軸都不垂直的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點(diǎn),線段
兩點(diǎn),線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,
,![]() 為坐標(biāo)原點(diǎn),且直線
為坐標(biāo)原點(diǎn),且直線![]() 與右準(zhǔn)線
與右準(zhǔn)線![]() 交于點(diǎn)
交于點(diǎn)![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)是否存在實(shí)數(shù)![]() ,使得
,使得![]() 恒成立?若存在,求實(shí)數(shù)
恒成立?若存在,求實(shí)數(shù)![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2020年初,一場新冠肺炎疫情突如其來,在黨中央強(qiáng)有力的領(lǐng)導(dǎo)下,全國各地的醫(yī)務(wù)工作者迅速馳援湖北,以大無畏的精神沖在了抗擊疫情的第一線,迅速控制住疫情.但國外疫情嚴(yán)峻,輸入性病例逐漸增多,為了鞏固我國的抗疫成果,保護(hù)國家和人民群眾的生命安全,我國三家生物高科技公司各自組成A、B、C三個(gè)科研團(tuán)隊(duì)進(jìn)行加急疫苗研究,其研究方向分別是滅活疫苗、核酸疫苗和全病毒疫苗,根據(jù)這三家的科技實(shí)力和組成的團(tuán)隊(duì)成員,專家預(yù)測這A、B、C三個(gè)團(tuán)隊(duì)未來六個(gè)月中研究出合格疫苗并用于臨床接種的概率分別為![]() ,
,![]() ,
,![]() ,且三個(gè)團(tuán)隊(duì)是否研究出合格疫苗相互獨(dú)立.
,且三個(gè)團(tuán)隊(duì)是否研究出合格疫苗相互獨(dú)立.
(1)求六個(gè)月后A,B兩個(gè)團(tuán)隊(duì)恰有一個(gè)研究出合格疫苗并用于臨床接種的概率;
(2)設(shè)六個(gè)月后研究出合格疫苗并用于臨床接種的團(tuán)隊(duì)個(gè)數(shù)為X,求X的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的焦距為4.且過點(diǎn)
的焦距為4.且過點(diǎn)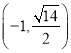 .
.
(1)求橢圓E的方程;
(2)設(shè)![]() ,
,![]() ,
,![]() ,過B點(diǎn)且斜率為
,過B點(diǎn)且斜率為![]() 的直線l交橢圓E于另一點(diǎn)M,交x軸于點(diǎn)Q,直線AM與直線
的直線l交橢圓E于另一點(diǎn)M,交x軸于點(diǎn)Q,直線AM與直線![]() 相交于點(diǎn)P.證明:
相交于點(diǎn)P.證明:![]() (O為坐標(biāo)原點(diǎn)).
(O為坐標(biāo)原點(diǎn)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l:![]() 和橢圓
和橢圓![]() :
:![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]()
(1)當(dāng)直線l過橢圓![]() 的左焦點(diǎn)和上頂點(diǎn)時(shí),求直線l的方程
的左焦點(diǎn)和上頂點(diǎn)時(shí),求直線l的方程
(2)點(diǎn)![]() 在
在![]() 上,若
上,若![]() ,求
,求![]() 面積的最大值:
面積的最大值:
(3)如果原點(diǎn)O到直線l的距離是![]() ,證明:
,證明:![]() 為直角三角形.
為直角三角形.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某地有一塊半徑為R的扇形AOB公園,其中O為扇形所在圓的圓心,AOB=![]() ,OA,OB,
,OA,OB,![]() 為公園原有道路.為滿足市民觀賞和健身的需要,市政部門擬在
為公園原有道路.為滿足市民觀賞和健身的需要,市政部門擬在![]() 上選取一點(diǎn)M,新建道路OM及與OA平行的道路MN(點(diǎn)N在線段OB上),設(shè)AOM=
上選取一點(diǎn)M,新建道路OM及與OA平行的道路MN(點(diǎn)N在線段OB上),設(shè)AOM=![]() .
.

(1)如何設(shè)計(jì),才能使市民從點(diǎn)O出發(fā)沿道路OM,MN行走至點(diǎn)N所經(jīng)過的路徑最長?請說明理由;
(2)如何設(shè)計(jì),才能使市民從點(diǎn)A出發(fā)沿道路![]() ,MN行走至點(diǎn)N所經(jīng)過的路徑最長?請說明理由.
,MN行走至點(diǎn)N所經(jīng)過的路徑最長?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
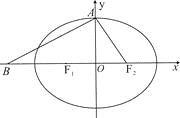
【題目】設(shè)橢圓![]() 的左、右焦點(diǎn)分別為
的左、右焦點(diǎn)分別為![]() ,上頂點(diǎn)為
,上頂點(diǎn)為![]() ,離心率為
,離心率為![]() , 在
, 在![]() 軸負(fù)半軸上有一點(diǎn)
軸負(fù)半軸上有一點(diǎn)![]() ,且
,且![]()
(1)若過![]() 三點(diǎn)的圓 恰好與直線
三點(diǎn)的圓 恰好與直線![]() 相切,求橢圓C的方程;
相切,求橢圓C的方程;
(2)在(1)的條件下,過右焦點(diǎn)![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓C交于
與橢圓C交于![]() 兩點(diǎn),在
兩點(diǎn),在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使得以
,使得以![]() 為鄰邊的平行四邊形是菱形,如果存在,求出
為鄰邊的平行四邊形是菱形,如果存在,求出![]() 的取值范圍;如果不存在,說明理由.
的取值范圍;如果不存在,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com