分析:(Ⅰ)利用
an=(Ⅱ)用等比數列的定義證明
=q;先判斷公比是否為1,再選擇等比數列的前 n 項和公式求解
(Ⅲ)裂項求和求T
n,判斷T
n-T
n+1的正負,證明數列{T
n}的單調性,求出T
n的最值
>,解k
解答:解:(Ⅰ)當n=1時,a
1=S
1=5,(1分)
當n≥2時,
an=Sn-Sn-1=[n2-(n-1)2]+[n-(n-1)]=
(2n-1)+=3n+2.(2分)
又a
1=5滿足a
n=3n+2,(3分)
∴a
n=3n+2?(n∈N
*).(4分)
∵a
n-a
n-1=3n+2-[3(n-1)+2]=3(n≥2,n∈N
*),
∴數列a
n是以5為首項,3為公差的等差數列.(5分)
(Ⅱ)由已知得
bn=2an(n∈N
*),(6分)
∵
==2an+1-an=23=8(n∈N
*),(7分)
又
b1=2a1=32,
∴數列b
n是以32為首項,8為公比的等比數列.(8分)
∴數列b
n前n項和為
=(8n-1).(9分)
(Ⅲ)
cn===(-)(10分)
∴
Tn=[(-)+(-)++(-)]=
(1-)=.(11分)
∵
Tn+1-Tn=>0(n∈N
*),
∴T
n單調遞增.
∴
(Tn)min=T1=.(12分)
∴
>,解得k<19,因為k是正整數,∴k
max=18.(13分)
點評:當已知條件中含有S
n,會用
an=,由前n項和求通項公式,是高考對數列部分的考查的重點,本題綜合考查由和求項、等差數列的證明,等比數列的求和公式,及裂項求和,把握好裂項相消后余下的項.



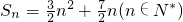 .
.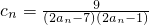 ,數列{cn}的前n項和為Tn,求使不等式Tn>
,數列{cn}的前n項和為Tn,求使不等式Tn>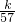 對一切n∈N*都成立的最大正整數k的值.
對一切n∈N*都成立的最大正整數k的值. .
. ,數列{cn}的前n項和為Tn,求使不等式Tn>
,數列{cn}的前n項和為Tn,求使不等式Tn> 對一切n∈N*都成立的最大正整數k的值.
對一切n∈N*都成立的最大正整數k的值. .
. ,數列{cn}的前n項和為Tn,求使不等式Tn>
,數列{cn}的前n項和為Tn,求使不等式Tn> 對一切n∈N*都成立的最大正整數k的值.
對一切n∈N*都成立的最大正整數k的值.