
分析 (1)討論a=0,a≠0時,運用奇偶性定義,即可判斷;
(2)運用配方法,對a討論,若a≤-$\frac{1}{2}$,a>-$\frac{1}{2}$,根據單調性,即可求得最小值.
解答 解:(1)當a=0時,函數f(-x)=(-x)2+|-x|+1=f(x),此時f(x)為偶函數.
當a≠0時,f(a)=a2+1,f(-a)=a2+2|a|+1,f(-a)≠f(a).
且f(-x)=x2+|-x-a|+1≠±f(x),
此時函數f(x)為非奇非偶函數.
(2)當x≥a時,函數$f(x)={x^2}+x-a+1={(x+\frac{1}{2})^2}-a+\frac{3}{4}$.
若a≤-$\frac{1}{2}$,則函數f(x)在[a,+∞)上的最小值為$f(-\frac{1}{2})=\frac{3}{4}-a$.
若a>-$\frac{1}{2}$,則函數f(x)在[a,+∞)上單調遞增,
從而,函數f(x)在[a,+∞)上的最小值為f(a)=a2+1.
綜上,當a≤-$\frac{1}{2}$時,函數f(x)的最小值是$\frac{3}{4}$-a.
當a>-$\frac{1}{2}$時,函數f(x)的最小值是a2+1.
點評 本題考查函數的奇偶性和最值的求法,注意運用分類討論的思想方法,考查運算能力,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
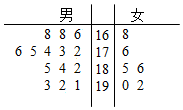 某公司從大學招收畢業生,經過綜合測試,錄用了14名男生和6名女生,這20名畢業生的測試成績如莖葉圖所示(單位:分).公司規定:成績在180分以上者到甲部門工作,180分以下者到乙部門工作,另外只有成績高于180分的男生才能擔任助理工作.
某公司從大學招收畢業生,經過綜合測試,錄用了14名男生和6名女生,這20名畢業生的測試成績如莖葉圖所示(單位:分).公司規定:成績在180分以上者到甲部門工作,180分以下者到乙部門工作,另外只有成績高于180分的男生才能擔任助理工作. 查看答案和解析>>
科目:高中數學 來源: 題型:解答題
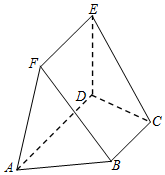 如圖,在五面體ACDEF中,已知DE⊥平面ABCD,AD∥BC,∠BAD=60°,AB=4,DE=EF=2.
如圖,在五面體ACDEF中,已知DE⊥平面ABCD,AD∥BC,∠BAD=60°,AB=4,DE=EF=2.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{9\sqrt{2}}{2}$ | B. | $\frac{9\sqrt{2}}{4}$ | C. | $\frac{9\sqrt{2}}{8}$ | D. | 9$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
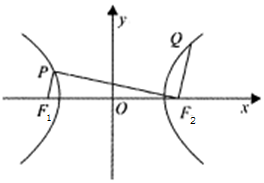 設F1,F2為雙曲線C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦點,P,Q分別為雙曲線左、右支上的點,若$\overrightarrow{Q{F_2}}$=2$\overrightarrow{P{F_1}}$,且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$═0,則雙曲線的離心率為( )
設F1,F2為雙曲線C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦點,P,Q分別為雙曲線左、右支上的點,若$\overrightarrow{Q{F_2}}$=2$\overrightarrow{P{F_1}}$,且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$═0,則雙曲線的離心率為( )| A. | $\frac{{\sqrt{15}}}{3}$ | B. | $\frac{{\sqrt{17}}}{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=3x+1 | B. | f(x)=$\frac{1}{x}$ | C. | f(x)=1-$\frac{1}{x}$ | D. | f(x)=x3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com