
已知銳角△ABC中, 分別為角A、B、C所對的邊,且
分別為角A、B、C所對的邊,且 .
.
(1) 求角C的大小;(2)若 ,且
,且
 ,求
,求 的值.
的值.
科目:高中數學 來源: 題型:解答題
已知△ABC中,內角A,B,C的對邊分別為a,b,c,其中a=2,c= .
.
(1)若sinC=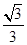 ,求sinA的值;
,求sinA的值;
(2)設f(C)= sinCcosC-cos2C,求f(C)的取值范圍.
sinCcosC-cos2C,求f(C)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2013·重慶高考)在△ABC中,內角A,B,C的對邊分別是a,b,c,且a2=b2+c2+ ab.
ab.
(1)求A.
(2)設a= ,S為△ABC的面積,求S+3cosBcosC的最大值,并指出此時B的值.
,S為△ABC的面積,求S+3cosBcosC的最大值,并指出此時B的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com