
【題目】如圖,已知點F為拋物線C:![]() (
(![]() )的焦點,過點F的動直線l與拋物線C交于M,N兩點,且當直線l的傾斜角為45°時,
)的焦點,過點F的動直線l與拋物線C交于M,N兩點,且當直線l的傾斜角為45°時,![]() .
.
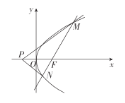
(1)求拋物線C的方程.
(2)試確定在x軸上是否存在點P,使得直線PM,PN關于x軸對稱?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】(1)![]() (2)存在唯一的點
(2)存在唯一的點![]() ,使直線PM,PN關于x軸對稱
,使直線PM,PN關于x軸對稱
【解析】
(1)當直線l的傾斜角為45°,則![]() 的斜率為1,則直線方程為
的斜率為1,則直線方程為![]() ,聯立直線與拋物線方程,利用韋達定理可得
,聯立直線與拋物線方程,利用韋達定理可得![]() ,根據焦點弦公式
,根據焦點弦公式![]() ,求出
,求出![]() 的值,即可得到拋物線方程.
的值,即可得到拋物線方程.
(2)假設滿足條件的點P存在,設![]() ,當直線l不與x軸垂直時,設l的方程為
,當直線l不與x軸垂直時,設l的方程為![]() (
(![]() ),聯立直線與拋物線方程,消元,列出韋達定理,因為直線PM,PN關于x軸對稱,所以
),聯立直線與拋物線方程,消元,列出韋達定理,因為直線PM,PN關于x軸對稱,所以![]() ,即可求出
,即可求出![]() 的值. 當直線l與x軸垂直時,由拋物線的對稱性,易知PM,PN關于x軸對稱,此時只需P與焦點F不重合即可.
的值. 當直線l與x軸垂直時,由拋物線的對稱性,易知PM,PN關于x軸對稱,此時只需P與焦點F不重合即可.
解:(1)當直線l的傾斜角為45°,則![]() 的斜率為1,
的斜率為1,
![]() ,
,![]() 的方程為
的方程為![]() .
.
由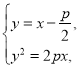 得
得![]() .
.
設![]() ,
,![]() ,則
,則![]() ,
,
∴![]() ,
,![]() ,
,
∴拋物線C的方程為![]() .
.
(2)假設滿足條件的點P存在,設![]() ,由(1)知
,由(1)知![]() ,
,
①當直線l不與x軸垂直時,設l的方程為![]() (
(![]() ),
),
由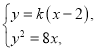 得
得![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
∵直線PM,PN關于x軸對稱,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() 時,此時
時,此時![]() .
.
②當直線l與x軸垂直時,由拋物線的對稱性,
易知PM,PN關于x軸對稱,此時只需P與焦點F不重合即可.
綜上,存在唯一的點![]() ,使直線PM,PN關于x軸對稱.
,使直線PM,PN關于x軸對稱.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:高中數學 來源: 題型:
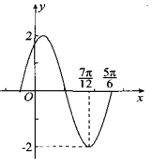
【題目】如圖是函數![]() 的部分圖象,將函數f(x)的圖象向右平移
的部分圖象,將函數f(x)的圖象向右平移![]() 個單位長度得到g(x)的圖象,給出下列四個命題:
個單位長度得到g(x)的圖象,給出下列四個命題:
①函數f(x)的表達式為![]() ;
;
②g(x)的一條對稱軸的方程可以為![]() ;
;
③對于實數m,恒有![]() ;
;
④f(x)+g(x)的最大值為2.其中正確的個數有( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求實數a的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“大眾創業,萬眾創新”是李克強總理在本屆政府工作報告中向全國人民發出的口號.某生產企業積極響應號召,大力研發新產品,為了對新研發的一批產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到一組銷售數據![]()
![]() ,如表所示:
,如表所示:
試銷單價 | 4 | 5 | 6 | 7 | 8 | 9 |
產品銷量 | q | 84 | 83 | 80 | 75 | 68 |
已知![]() ,
,![]() .
.
(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)已知變量![]() ,
,![]() 具有線性相關關系,求產品銷量
具有線性相關關系,求產品銷量![]() (件)關于試銷單價
(件)關于試銷單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(Ⅲ)用![]() 表示用(Ⅱ)中所求的線性回歸方程得到的與
表示用(Ⅱ)中所求的線性回歸方程得到的與![]() 對應的產品銷量的估計值.當銷售數據
對應的產品銷量的估計值.當銷售數據![]() 對應的殘差的絕對值
對應的殘差的絕對值![]() 時,則將銷售數據
時,則將銷售數據![]() 稱為一個“好數據”.現從6個銷售數據中任取2個,求“好數據”至少有一個的概率.
稱為一個“好數據”.現從6個銷售數據中任取2個,求“好數據”至少有一個的概率.
(參考公式:線性回歸方程中![]() ,
,![]() 的最小二乘估計分別為
的最小二乘估計分別為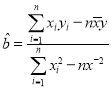 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+![]() )(A>0,ω>0,|
)(A>0,ω>0,|![]() |<
|<![]() )的部分圖象如圖所示.
)的部分圖象如圖所示.
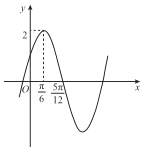
(Ⅰ)求f(x)的解析式;
(Ⅱ)若對于任意的x∈[0,m],f(x)≥1恒成立,求m的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+(a-2)lnx+1(a∈R).
(1)若函數在點(1,f(1))處的切線平行于直線y=4x+3,求a的值;
(2)令c(x)=f(x)+(3-a)lnx+2a,討論c(x)的單調性;
(3)a=1時,函數y=f(x)圖象上的所有點都落在區域![]() 內,求實數t的取值范圍.
內,求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com