
【題目】已知![]() .
.
(I)討論![]() 的單調(diào)性;
的單調(diào)性;
(II)當(dāng)![]() 有最大值,且最大值大于
有最大值,且最大值大于![]() 時,求a的取值范圍.
時,求a的取值范圍.
【答案】(Ⅰ)詳見解析;(Ⅱ)![]()
【解析】試題分析:
(1)由題已知函數(shù)的解析式(注意定義域),可運用導(dǎo)數(shù)求出函數(shù)的單調(diào)區(qū)間。即: ![]() 為函數(shù)的增區(qū)間,反之為減區(qū)間。由導(dǎo)函數(shù)中含有字母參數(shù),需分類討論;
為函數(shù)的增區(qū)間,反之為減區(qū)間。由導(dǎo)函數(shù)中含有字母參數(shù),需分類討論;
(2)由題給出了函數(shù)的最大值的范圍大于![]() ,再結(jié)合(1)已知函數(shù)的單調(diào)區(qū)間,可對應(yīng)單調(diào)性,表示出函數(shù)的最大值,從而建立不等式lna+a-1<0,需構(gòu)造函數(shù)利用單調(diào)性解出不等式的解,而求出
,再結(jié)合(1)已知函數(shù)的單調(diào)區(qū)間,可對應(yīng)單調(diào)性,表示出函數(shù)的最大值,從而建立不等式lna+a-1<0,需構(gòu)造函數(shù)利用單調(diào)性解出不等式的解,而求出![]() 的取值范圍。
的取值范圍。
試題解析:
(Ⅰ)f(x)=lnx+a(1﹣x)的定義域為(0,+∞),∴f′(x)=![]() ﹣a=
﹣a=![]() ,
,
若a≤0,則f′(x)>0,∴函數(shù)f(x)在(0,+∞)上單調(diào)遞增,
若a>0,則當(dāng)x∈(0,![]() )時,f′(x)>0,
)時,f′(x)>0,
當(dāng)x∈(![]() ,+∞)時,f′(x)<0,所以f(x)在(0,
,+∞)時,f′(x)<0,所以f(x)在(0,![]() )上單調(diào)遞增,在(
)上單調(diào)遞增,在(![]() ,+∞)上單調(diào)遞減,
,+∞)上單調(diào)遞減,
(Ⅱ)由(Ⅰ)知,當(dāng)a≤0時,f(x)在(0,+∞)上無最大值;
當(dāng)a>0時,f(x)在x=![]() 取得最大值,最大值為f(
取得最大值,最大值為f(![]() )=﹣lna+a-1,
)=﹣lna+a-1,
∵f(![]() )>2a﹣2,∴l(xiāng)na+a-1<0,
)>2a﹣2,∴l(xiāng)na+a-1<0,
令g(a)=lna+a-1,∵g(a)在(0,+∞)單調(diào)遞增,g(1)=0,
∴當(dāng)0<a<1時,g(a)<0,當(dāng)a>1時,g(a)>0,∴a的取值范圍為(0,1).


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】首屆世界低碳經(jīng)濟(jì)大會在南昌召開,本屆大會以“節(jié)能減排,綠色生態(tài)”為主題.某單位在國家科研部門的支持下,進(jìn)行技術(shù)攻關(guān),采用了新工藝,把二氧化碳轉(zhuǎn)化為一種可利用的化工產(chǎn)品.已知該單位每月的處理量最少為300噸,最多為600噸,月處理成本y(元)與月處理量x(噸)之間的函數(shù)關(guān)系可近似地表示為 ![]() ,且每處理一噸二氧化碳得到可利用的化工產(chǎn)品價值為200元.
,且每處理一噸二氧化碳得到可利用的化工產(chǎn)品價值為200元.
(1)該單位每月處理量為多少噸時,才能使每噸的平均處理成本最低?
(2)該單位每月能否獲利?如果獲利,求出最大利潤;如果不獲利,則需要國家至少補(bǔ)貼多少元才能使該單位不虧損?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=lg(x2+ax﹣a﹣1),給出下列命題:
①函數(shù)f(x)有最小值;
②當(dāng)a=0時,函數(shù)f(x)的值域為R;
③若函數(shù)f(x)在區(qū)間(﹣∞,2]上單調(diào)遞減,則實數(shù)a的取值范圍是a≤﹣4.
其中正確的命題是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若以曲線![]() 上任意一點
上任意一點![]() 為切點作切線
為切點作切線![]() ,曲線上總存在異于
,曲線上總存在異于![]() 的點
的點![]() ,以點
,以點![]() 為切點作切線
為切點作切線![]() ,且
,且![]() ,則稱曲線
,則稱曲線![]() 具有“可平行性”,現(xiàn)有下列命題:
具有“可平行性”,現(xiàn)有下列命題:
①函數(shù)![]() 的圖象具有“可平行性”;
的圖象具有“可平行性”;
②定義在![]() 的奇函數(shù)
的奇函數(shù)![]() 的圖象都具有“可平行性”;
的圖象都具有“可平行性”;
③三次函數(shù)![]() 具有“可平行性”,且對應(yīng)的兩切點
具有“可平行性”,且對應(yīng)的兩切點![]() ,
, ![]() 的橫坐標(biāo)滿足
的橫坐標(biāo)滿足![]() ;
;
④要使得分段函數(shù) 的圖象具有“可平行性”,當(dāng)且僅當(dāng)
的圖象具有“可平行性”,當(dāng)且僅當(dāng)![]() .
.
其中的真命題個數(shù)有()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 平面
平面![]() ,
,![]() 分別是
分別是![]() 的中點,
的中點,![]() ,
,![]() .
.
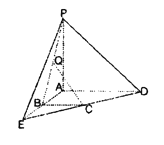
(1)求二面角![]() 的余弦值;
的余弦值;
(2)點![]() 是線段
是線段![]() 上的動點,當(dāng)直線
上的動點,當(dāng)直線![]() 與
與![]() 所成的角最小時,求線段
所成的角最小時,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() (
(![]() 為自然對數(shù)的底數(shù)),
為自然對數(shù)的底數(shù)),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的極值點,且直線
的極值點,且直線![]() 分別與函數(shù)
分別與函數(shù)![]() 和
和![]() 的圖象交于
的圖象交于![]() ,求
,求![]() 兩點間的最短距離;
兩點間的最短距離;
(2)若![]() 時,函數(shù)
時,函數(shù)![]() 的圖象恒在
的圖象恒在![]() 的圖象上方,求實數(shù)
的圖象上方,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】把復(fù)數(shù)z的共軛復(fù)數(shù)記作 ![]() ,i為虛數(shù)單位,若z=1+i.
,i為虛數(shù)單位,若z=1+i.
(1)求復(fù)數(shù)(1+z) ![]() ;
;
(2)求(1+ ![]() )z2的模.
)z2的模.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,AB⊥AD,AD∥BC,AP=AB=AD=1.
(Ⅰ)若直線PB與CD所成角的大小為![]() ,求BC的長;
,求BC的長;
(Ⅱ)求二面角B-PD-A的余弦值.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com