
(本題滿分12分)某中學校本課程共開設了 共
共 門選修課,每個學生必須且只能選修
門選修課,每個學生必須且只能選修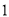 門選修課,現有該校的甲、乙、丙
門選修課,現有該校的甲、乙、丙 名學生.
名學生.
(Ⅰ)求這 名學生選修課所有選法的總數;
名學生選修課所有選法的總數;
(Ⅱ)求恰有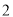 門選修課沒有被這
門選修課沒有被這 名學生選擇的概率;
名學生選擇的概率;
(Ⅲ)求 選修課被這
選修課被這 名學生選擇的人數
名學生選擇的人數 的分布列和數學期望.
的分布列和數學期望.
(Ⅰ)64 ;(Ⅱ)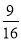 ;(Ⅲ)見解析
;(Ⅲ)見解析
【解析】
試題分析:(Ⅰ)由分步計數原理得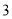 名學生選修課所有選法的總數為
名學生選修課所有選法的總數為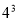 種;(Ⅱ)利用古典概型概率計算公式先求出事件所包含的基本事件個數,先從4門課程中選2門,其次從3名學生中選2人,再從所選2門課程中選1門共有
種;(Ⅱ)利用古典概型概率計算公式先求出事件所包含的基本事件個數,先從4門課程中選2門,其次從3名學生中選2人,再從所選2門課程中選1門共有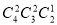 種;(Ⅲ)求解離散型隨機變量X的分布列的步驟:①理解X的意義,寫出X可能取的全部值;②求X取每個值的概率;③寫出X的分布列;④利用期望定義得出
種;(Ⅲ)求解離散型隨機變量X的分布列的步驟:①理解X的意義,寫出X可能取的全部值;②求X取每個值的概率;③寫出X的分布列;④利用期望定義得出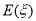
試題解析:(Ⅰ)每個學生有四個不同選擇,根據分步計數原理,選法總數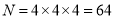 2分
2分
(Ⅱ)設“恰有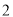 門選修課沒有被這
門選修課沒有被這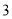 名學生選擇”為事件
名學生選擇”為事件 ,則
,則
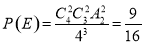 ,即恰有
,即恰有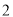 門選修課沒有被這
門選修課沒有被這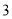 名學生選擇的概率為
名學生選擇的概率為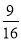 . 5分
. 5分
(Ⅲ)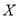 的所有可能取值為
的所有可能取值為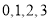 ,且
,且
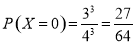 ,
,  ,
,
 ,
, 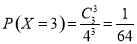 9分
9分
所以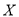 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
所以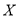 的數學期望
的數學期望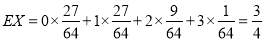 . 12分
. 12分
或:因為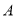 選修課被每位學生選中的概率均為
選修課被每位學生選中的概率均為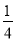 ,沒被選中的概率均為
,沒被選中的概率均為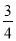 .
.
所以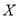 的所有可能取值為
的所有可能取值為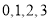 ,且
,且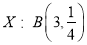 ,
,
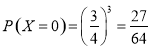 ,
,  ,
,
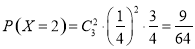 ,
, 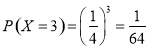 9分
9分
所以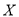 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
所以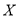 的數學期望
的數學期望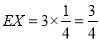 . 12分
. 12分
考點:古典概型、分布列、期望


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源:2014-2015學年河北邢臺一中高二上學期期中考試文科數學試卷(解析版) 題型:選擇題
已知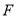 是拋物線
是拋物線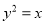 的焦點,
的焦點,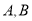 是該拋物線上的兩點,
是該拋物線上的兩點,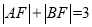 ,則線段
,則線段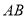 的中點到
的中點到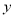 軸的距離為 ( )
軸的距離為 ( )
A.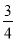 B.1 C.
B.1 C.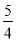 D.
D.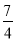
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省山一等七校高三12月聯考理科數學試卷(解析版) 題型:選擇題
已知三個正態分布密度函數 (
(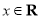 ,
,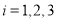 )的圖象如圖
)的圖象如圖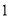 所示,則( )
所示,則( )

A. ,
,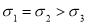
B.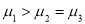 ,
,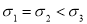
C. ,
,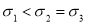
D.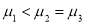 ,
,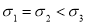
查看答案和解析>>
科目:高中數學 來源:2014-2015學年廣東省肇慶市畢業班第一次統一檢測文科數學試卷(解析版) 題型:選擇題
執行如圖所示的程序框圖輸出的結果是
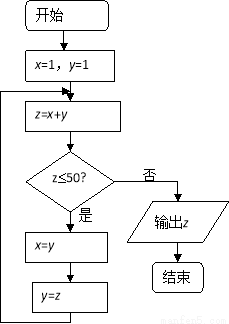
A.55 B.65
C.78 D.89
查看答案和解析>>
科目:高中數學 來源:2014-2015學年福建省四地六校高三上學期第三次月考文科數學試卷(解析版) 題型:選擇題
程序框圖如下圖所示,則輸出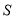 的值為( )
的值為( )
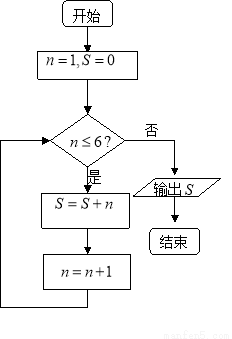
A.15 B.21 C.22 D.28
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com