
【題目】已知函數![]() ,(
,( ![]() )是偶函數.
)是偶函數.
(1)求![]() 的值;
的值;
(2)設函數![]() ,其中
,其中![]() .若函數
.若函數![]() 與
與![]() 的圖象有且只有一個交點,求
的圖象有且只有一個交點,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分別是AC、AD上的動點,且![]()
(1)求證:不論![]() 為何值,總有平面BEF⊥平面ABC;
為何值,總有平面BEF⊥平面ABC;
(2)當λ為何值時,平面BEF⊥平面ACD ?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,圓
,圓![]() .
.
(Ⅰ)若直線![]() 過點
過點![]() 且到圓心
且到圓心![]() 的距離為1,求直線
的距離為1,求直線![]() 的方程;
的方程;
(Ⅱ)設過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(
兩點(![]() 的斜率為正),當
的斜率為正),當![]() 時,求以線段
時,求以線段![]() 為直徑的圓的方程.
為直徑的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產某種零件,每個零件的成本為40元,出廠單價定為60元.該廠為鼓勵銷售商訂購,決定當一次訂購量超過100個時,每多訂購一個,訂購的全部零件的出廠單價就降低0.02元,但實際出廠單價不能低于51元.
(1)當一次訂購量為多少個時,零件的實際出廠單價恰降為51元?
(2)設一次訂購量為![]() 個,零件的實際出廠單價為
個,零件的實際出廠單價為![]() 元,寫出函數
元,寫出函數![]() 的表達式;
的表達式;
(3)當銷售商一次訂購500個零件時,該廠獲得的利潤是多少元? (工廠售出一個零件的利潤=實際出廠單價-單件成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2 ![]() ,E,F分別是AD,PC的中點.
,E,F分別是AD,PC的中點.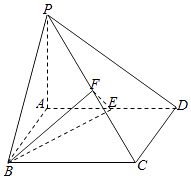
(1)證明:PC⊥平面BEF;
(2)求平面BEF與平面BAP所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常函數)是奇函數.
為常函數)是奇函數.
(1)判斷函數![]() 在
在![]() 上的單調性,并用定義法證明你的結論;
上的單調性,并用定義法證明你的結論;
(2)若對于區間![]() 上的任意
上的任意![]() 值,使得
值,使得![]() 不等式恒成立,求實數
不等式恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖動直線l:y=b與拋物線y2=4x交于點A,與橢圓 ![]() =1交于拋物線右側的點B,F為拋物線的焦點,則|AF|+|BF|+|AB|的最大值為( )
=1交于拋物線右側的點B,F為拋物線的焦點,則|AF|+|BF|+|AB|的最大值為( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com