
已知正項數列{ }的前
}的前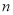 項和為
項和為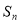 ,且
,且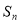 ,
, ,
,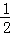 成等差數列.
成等差數列.
(1)證明數列{ }是等比數列;
}是等比數列;
(2)若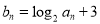 ,求數列
,求數列 的前
的前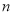 項和
項和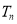 .
.
(1)證明見解析;(2)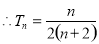
【解析】
試題分析:(1)證明一個數列是否為等差數列的基本方法有兩種:一是定義法:證明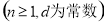 ;二是等差中項法,證明
;二是等差中項法,證明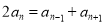 ,若證明一個數列不是等差數列,則只需舉出反例即可;(2)等比數列基本量的求解是等比數列的一類基本問題,解決這類問題的關鍵在于熟練掌握等比數列的有關公式并能靈活運用,(3)觀測數列的特點形式,看使用什么方法求和.使用裂項法求和時,要注意正負項相消時消去了哪些項,保留了哪些項,切不可漏寫未被消去的項,未被消去的項有前后對稱的特點,實質上造成正負相消是此法的根源和目的.
,若證明一個數列不是等差數列,則只需舉出反例即可;(2)等比數列基本量的求解是等比數列的一類基本問題,解決這類問題的關鍵在于熟練掌握等比數列的有關公式并能靈活運用,(3)觀測數列的特點形式,看使用什么方法求和.使用裂項法求和時,要注意正負項相消時消去了哪些項,保留了哪些項,切不可漏寫未被消去的項,未被消去的項有前后對稱的特點,實質上造成正負相消是此法的根源和目的.
試題解析:【解析】
(1)證明:由題意知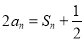
當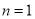 時,
時,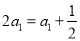 ,
,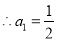
當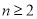 時,
時,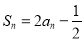 ,
,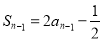
兩式相減得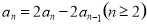 ,即
,即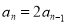
由于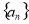 為正項數列,
為正項數列,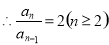
即數列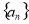 從第二項起,每一項與它前一項之比都是同一個常數2
從第二項起,每一項與它前一項之比都是同一個常數2
 數列
數列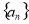 是以
是以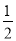 為首項,以2為公比的等比數列
為首項,以2為公比的等比數列
由(1)知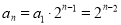 ,
,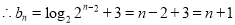
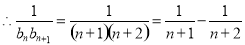
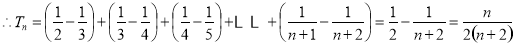 .
.
考點:1、證明數列為等比數列;2、裂項求和.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源:2015屆山東省菏澤市高三上學期期中聯考文科數學試卷(解析版) 題型:選擇題
函數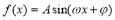 (其中
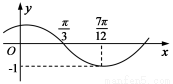
(其中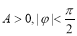 )的圖象如圖所示,為了得到
)的圖象如圖所示,為了得到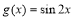 的圖象,則只要將f (x)的圖象( )
的圖象,則只要將f (x)的圖象( )
A.向右平移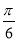 個單位長度
個單位長度
B.向右平移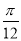 個單位長度
個單位長度
C.向左平移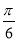 個單位長度
個單位長度
D.向左平移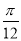 個單位長度
個單位長度
查看答案和解析>>
科目:高中數學 來源:2015屆山東省高三第一次檢測理科數學試卷(解析版) 題型:選擇題
為了得到 的圖像,只需要將
的圖像,只需要將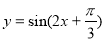 ( )
( )
A.向左平移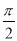 個單位 B.向右平移
個單位 B.向右平移 個單位
個單位
C.向左平移 個單位 D.向右平移
個單位 D.向右平移 個單位
個單位
查看答案和解析>>
科目:高中數學 來源:2015屆山東省高三第一次檢測文科數學試卷(解析版) 題型:選擇題
已知函數f(x)=sin x- x(x∈[0,π]),那么下列結論正確的是 ( ).
x(x∈[0,π]),那么下列結論正確的是 ( ).
A.f(x)在 上是增函數
上是增函數
B.f(x)在 上是減函數
上是減函數
C.?x∈ ,
,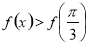
D.?x∈ ,
, 。
。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com