
【題目】已知橢圓![]() 的焦點在
的焦點在![]() 軸上,且橢圓
軸上,且橢圓![]() 的焦距為2.
的焦距為2.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,過
,過![]() 作
作![]() 軸且與橢圓
軸且與橢圓![]() 交于另一點
交于另一點![]() ,
, ![]() 為橢圓
為橢圓![]() 的右焦點,求證:三點
的右焦點,求證:三點![]() 在同一條直線上.
在同一條直線上.
 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案科目:高中數學 來源: 題型:
【題目】為調查某地區老人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
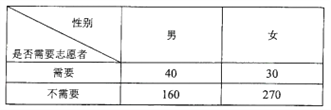
(Ⅰ)估計該地區老年人中,需要志愿者提供幫助的老年人的比例;
(Ⅱ)能否有![]() 的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
(Ⅲ)根據(Ⅱ)的結論,能否提供更好的調查方法來估計該地區的老年人中,需要志愿者提供幫助的老年人的比例?說明理由.
附: 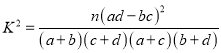
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知城![]() 和城
和城![]() 相距
相距![]() ,現計劃以
,現計劃以![]() 為直徑的半圓上選擇一點
為直徑的半圓上選擇一點![]() (不與點
(不與點![]() ,
, ![]() 重合)建造垃圾處理廠.垃圾處理廠對城市的影響度與所選地點到城市的距離有關,對城
重合)建造垃圾處理廠.垃圾處理廠對城市的影響度與所選地點到城市的距離有關,對城![]() 和城
和城![]() 的總影響度為對城
的總影響度為對城![]() 與城
與城![]() 的影響度之和.記點到
的影響度之和.記點到![]() 城
城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理廠對城
處的垃圾處理廠對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() .統計調查表明:垃圾處理廠對城
.統計調查表明:垃圾處理廠對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比例關系,比例系數為4;對城
的距離的平方成反比例關系,比例系數為4;對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比例關系,比例系數為
的距離的平方成反比例關系,比例系數為![]() .當垃圾處理廠建在
.當垃圾處理廠建在![]() 的中點時,對城
的中點時,對城![]() 和城
和城![]() 的總影響度為0.065.
的總影響度為0.065.
(1)將![]() 表示成
表示成![]() 的函數.
的函數.
(2)討論(1)中函數的單調性,并判斷在![]() 上是否存在一點,使建在此處的垃圾處理廠對城
上是否存在一點,使建在此處的垃圾處理廠對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點到城
的總影響度最小?若存在,求出該點到城![]() 的距離;若不存在,請說明理由.
的距離;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國內某汽車品牌一個月內被消費者投訴的次數用![]() 表示,據統計,隨機變量
表示,據統計,隨機變量![]() 的概率分布如下:
的概率分布如下:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值;
的值;
(2)假設一月與二月被消費者投訴的次數互不影響,求該汽車品牌在這兩個月內被消費者投訴![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以坐標原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.已知點
軸的非負半軸為極軸建立極坐標系.已知點![]() 的極坐標為
的極坐標為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() 為參數).
為參數).
(1)直線![]() 過
過![]() 且與曲線
且與曲線![]() 相切,求直線
相切,求直線![]() 的極坐標方程;
的極坐標方程;
(2)點![]() 與點
與點![]() 關于
關于![]() 軸對稱,求曲線
軸對稱,求曲線![]() 上的點到點
上的點到點![]() 的距離的取值范圍.
的距離的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·全國卷Ⅲ文,18)某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:℃)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間[20,25),需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
最高氣溫 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區間的頻率估計最高氣溫位于該區間的概率.
(1)估計六月份這種酸奶一天的需求量不超過300瓶的概率;
(2)設六月份一天銷售這種酸奶的利潤為Y(單位:元).當六月份這種酸奶一天的進貨量為450瓶時,寫出Y的所有可能值,并估計Y大于零的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() 為參數).它與曲線
為參數).它與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求![]() 的長;
的長;
(2)在以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,設點
軸的正半軸為極軸建立極坐標系,設點![]() 的極坐標為
的極坐標為![]() ,求點
,求點![]() 到線段
到線段![]() 中點
中點![]() 的距離.
的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com