
【題目】為調查某地區老人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
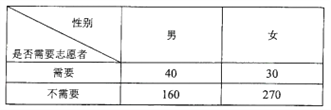
(Ⅰ)估計該地區老年人中,需要志愿者提供幫助的老年人的比例;
(Ⅱ)能否有![]() 的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
(Ⅲ)根據(Ⅱ)的結論,能否提供更好的調查方法來估計該地區的老年人中,需要志愿者提供幫助的老年人的比例?說明理由.
附: 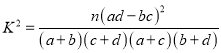
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1) ![]() ;(2) 有
;(2) 有![]() 的把握認為該地區的老年人是否需要幫助與性別有關;(3)采用分層抽樣方法比采用簡單隨機抽樣方法更好.
的把握認為該地區的老年人是否需要幫助與性別有關;(3)采用分層抽樣方法比采用簡單隨機抽樣方法更好.
【解析】試題分析:(1)由樣本的頻率估計總體的概率;(2)根據公式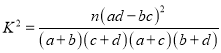 求
求![]() 的值,對比臨界值可得結論;(3)由(2)的結論知,該地區老年人是否需要幫助與性別有關,并且從樣本數據能看出該地區男性老年人與女性老年人中需要幫助的比例有明顯差異,因此在調查時可按性別分層抽樣.
的值,對比臨界值可得結論;(3)由(2)的結論知,該地區老年人是否需要幫助與性別有關,并且從樣本數據能看出該地區男性老年人與女性老年人中需要幫助的比例有明顯差異,因此在調查時可按性別分層抽樣.
試題解析:(Ⅰ)調查的500位老年人中有70位需要志愿者提供幫助,因此該地區老年人中,需要幫助的老年人的比例的估算值為![]() ;
;
(Ⅱ)![]() ,由于
,由于![]() .
.
所以有![]() 的把握認為該地區的老年人是否需要幫助與性別有關;
的把握認為該地區的老年人是否需要幫助與性別有關;
(Ⅲ)由(Ⅱ)的結論知,該地區老年人是否需要幫助與性別有關,并且從樣本數據能看出該地區男性老年人與女性老年人中需要幫助的比例有明顯差異,因此在調查時,先確定該地區老年人中男、女的比例,再把老年人分成男、女兩層并采用分層抽樣方法比采用簡單隨機抽樣方法更好.


 一課一練課時達標系列答案
一課一練課時達標系列答案 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:高中數學 來源: 題型:
【題目】據某市地產數據研究的數據顯示,2016年該市新建住宅銷售均價走勢如下圖所示,為抑制房價過快上漲,政府從8月采取宏觀調控措施,10月份開始房價得到很好的抑制.
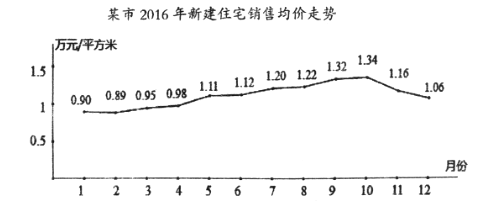
(1)地產數據研究院發現,3月至7月的各月均價![]() (萬元/平方米)與月份
(萬元/平方米)與月份![]() 之間具有較強的線性相關關系,試建立
之間具有較強的線性相關關系,試建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01);政府若不調控,依此相關關系預測第12月份該市新建住宅銷售均價;
的回歸方程(系數精確到0.01);政府若不調控,依此相關關系預測第12月份該市新建住宅銷售均價;
(2)地產數據研究院在2016年的12個月份中,隨機抽取三個月的數據作樣本分析,若關注所抽三個月份的所屬季度,記不同季度的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考數據: ![]() ,
, ![]() ,
, ![]() ;
;
回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為:
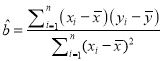 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了宣傳環保知識,舉辦了一次“環保知識知多少”的問卷調查活動(一
人答一份).現從回收的年齡在20~60歲的問卷中隨機抽取了100份,統計結果如下面的圖表所示.
年齡 分組 | 抽取份數 | 答對全卷 的人數 | 答對全卷的人數 占本組的概率 |
[20,30) | 40 | 28 | 0.7 |
[30,40) |
| 27 | 0.9 |
[40,50) | 10 | 4 |
|
[50,60] | 20 |
| 0.1 |

(1)分別求出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)從年齡在![]() 答對全卷的人中隨機抽取2人授予“環保之星”,求年齡在
答對全卷的人中隨機抽取2人授予“環保之星”,求年齡在![]() 的人中至少有1人被授予“環保之星”的概率.
的人中至少有1人被授予“環保之星”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為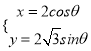 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,與直角坐標系
軸的正半軸為極軸,與直角坐標系![]() 取相同的單位長度建立極坐標系,曲線
取相同的單位長度建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)化曲線![]() 的方程為普通方程,并說明它們分別表示什么曲線;
的方程為普通方程,并說明它們分別表示什么曲線;
(2)設曲線![]() 與
與![]() 軸的一個交點的坐標為
軸的一個交點的坐標為![]() ,經過點
,經過點![]() 作斜率為1的直線,
作斜率為1的直線, ![]() 交曲線
交曲線![]() 于
于![]() 兩點,求線段
兩點,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線的頂點在坐標原點,焦點![]() 在
在![]() 軸上,過點
軸上,過點![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,線段
兩點,線段![]() 的長度為8,
的長度為8, ![]() 的中點到
的中點到![]() 軸的距離為3.
軸的距離為3.
(1)求拋物線的標準方程;
(2)設直線![]() 在
在![]() 軸上的截距為6,且拋物線交于
軸上的截距為6,且拋物線交于![]() 兩點,連結
兩點,連結![]() 并延長交拋物線的準線于點
并延長交拋物線的準線于點![]() ,當直線
,當直線![]() 恰與拋物線相切時,求直線
恰與拋物線相切時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從5名男生和4名女生中選出4人去參加座談會,問:
(1)如果4人中男生和女生各選2人,有多少種選法?
(2)如果男生中的甲與女生中的乙至少要有1人在內,有多少種選法?
(3)如果4人中必須既有男生又有女生,有多少種選法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦點在
的焦點在![]() 軸上,且橢圓
軸上,且橢圓![]() 的焦距為2.
的焦距為2.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,過
,過![]() 作
作![]() 軸且與橢圓
軸且與橢圓![]() 交于另一點
交于另一點![]() ,
, ![]() 為橢圓
為橢圓![]() 的右焦點,求證:三點
的右焦點,求證:三點![]() 在同一條直線上.
在同一條直線上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com