
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)若函數![]() 有兩個極值點,試判斷函數
有兩個極值點,試判斷函數![]() 的零點個數.
的零點個數.
【答案】(1) 當![]() 時,
時,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() 單調遞減;(2)存在3個零點.
單調遞減;(2)存在3個零點.
【解析】
(1)先確定![]() 的定義域,通過求導數解出其單調區間;
的定義域,通過求導數解出其單調區間;
(2)利用函數![]() 有極值,判斷
有極值,判斷![]() 的取值范圍,進而確定極值點的大小關系,得到
的取值范圍,進而確定極值點的大小關系,得到![]() 的單調區間,最后通過極值
的單調區間,最后通過極值![]() 的正負判斷出零點的個數.
的正負判斷出零點的個數.
(1)由題意可知函數![]() 的定義域為
的定義域為![]()
當![]() 時:
時:![]() ,所以
,所以![]() 單調遞增;
單調遞增;
當![]() 時:
時:![]() ,所以
,所以![]() 單調遞減;
單調遞減;
所以當![]() 時,
時,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() 單調遞減.
單調遞減.
(2)由題意得:![]() 有兩個不同的零點,即
有兩個不同的零點,即![]() 有兩個不同的根設為
有兩個不同的根設為![]() ,由(1)得
,由(1)得![]() 當
當![]() 時
時![]() 單調遞增;當
單調遞增;當![]() 時
時![]() 單調遞減;有
單調遞減;有![]() 當
當![]() 時
時![]() ,所以
,所以![]() 時,有
時,有![]() 使
使![]() 且函數
且函數![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,
單調遞增,
現只需比較![]() 的正負進而確定零點個數.
的正負進而確定零點個數.
有![]() 且
且![]() 且
且![]() ,即
,即![]() ,
,![]() .
.
令![]() 則
則 所以函數
所以函數![]() 在
在![]() 上單調增,所以
上單調增,所以![]() 時
時![]()
![]() 時
時![]() 又
又![]() 時
時![]() 時
時![]()
所以函數有三個零點.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,若滿足
,若滿足![]() ,則稱函數
,則稱函數![]() 為“
為“![]() 型函數”.
型函數”.
(1)判斷函數![]() 和
和![]() 是否為“
是否為“![]() 型函數”,并說明理由;
型函數”,并說明理由;
(2)設函數![]() ,記
,記![]() 為函數
為函數![]() 的導函數.
的導函數.
①若函數![]() 的最小值為1,求
的最小值為1,求![]() 的值;
的值;
②若函數![]() 為“
為“![]() 型函數”,求
型函數”,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學組織高二年級開展對某品牌西瓜市場調研活動.兩名同學經過了解得知此品牌西瓜,不僅便宜而且口味還不錯,并且每日的銷售量y(單位:千克)與銷售價格x(元/千克)滿足關系式:![]() ,其中
,其中![]() ,a為常數.已知銷售價格為5元/千克時,每日可售出此品牌西瓜11千克.若此品牌西瓜的成本為3元/千克,試確定銷售價格x的值,使該商場日銷售此品牌西瓜所獲得的利潤最大.
,a為常數.已知銷售價格為5元/千克時,每日可售出此品牌西瓜11千克.若此品牌西瓜的成本為3元/千克,試確定銷售價格x的值,使該商場日銷售此品牌西瓜所獲得的利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四面體![]() 的棱長滿足
的棱長滿足![]() ,
,![]() ,現將四面體
,現將四面體![]() 放入一個主視圖為等邊三角形的圓錐中,使得四面體
放入一個主視圖為等邊三角形的圓錐中,使得四面體![]() 可以在圓錐中任意轉動,則圓錐側面積的最小值為___________.
可以在圓錐中任意轉動,則圓錐側面積的最小值為___________.
查看答案和解析>>
科目:高中數學 來源: 題型:
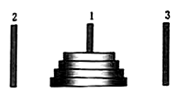
【題目】如圖所示,有三根針和套在一根針上的![]() 個金屬片,按下列規則,把金屬片從一根針上全部移到另一根針上.
個金屬片,按下列規則,把金屬片從一根針上全部移到另一根針上.
(1)每次只能移動一個金屬片;
(2)在每次移動過程中,每根針上較大的金屬片不能放在較小的金屬片上面.
將![]() 個金屬片從1號針移到3號針最少需要移動的次數記為
個金屬片從1號針移到3號針最少需要移動的次數記為![]() ,則
,則![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與x軸負半軸交于
與x軸負半軸交于![]() ,離心率
,離心率![]() .
.
(1)求橢圓C的方程;
(2)設直線![]() 與橢圓C交于
與橢圓C交于![]() 兩點,連接AM,AN并延長交直線x=4于
兩點,連接AM,AN并延長交直線x=4于![]() 兩點,若
兩點,若![]() ,直線MN是否恒過定點,如果是,請求出定點坐標,如果不是,請說明理由.
,直線MN是否恒過定點,如果是,請求出定點坐標,如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解高二年級學生某次數學考試成績的分布情況,從該年級的1120名學生中隨機抽取了100名學生的數學成績,發現都在![]() 內現將這100名學生的成績按照
內現將這100名學生的成績按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組后,得到的頻率分布直方圖如圖所示,則下列說法正確的是
分組后,得到的頻率分布直方圖如圖所示,則下列說法正確的是![]()
![]()

A. 頻率分布直方圖中a的值為![]()
B. 樣本數據低于130分的頻率為![]()
C. 總體的中位數![]() 保留1位小數
保留1位小數![]() 估計為
估計為![]() 分
分
D. 總體分布在![]() 的頻數一定與總體分布在
的頻數一定與總體分布在![]() 的頻數相等
的頻數相等
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】氣象意義上,從春季進入夏季的標志為:“連續5天的日平均溫度不低于22℃”.現有甲、乙、丙三地連續5天的日平均溫度的記錄數據(記錄數據都是正整數):
①甲地:5個數據的中位數為24,眾數為22;
②乙地:5個數據的中位數為27,總體均值為24;
③丙地:5個數據的中有一個數據是32,總體均值為26,總體方差為10.8;
則肯定進入夏季的地區的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,直線
中,直線![]() 經過點
經過點![]() ,傾斜角為
,傾斜角為![]() ,以原點為極點,
,以原點為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為曲線
的極坐標方程為曲線![]() .
.
(Ⅰ)寫出直線![]() 的參數方程及曲線
的參數方程及曲線![]() 的普通方程;
的普通方程;
(Ⅱ)求直線![]() 和曲線
和曲線![]() 的兩個交點到點
的兩個交點到點![]() 的距離的和與積.
的距離的和與積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com