已知函數f(x)=5x-5x2,記函數f1(x)=f(x),f2(x)=f[f1(x)],f3(x)=f[f2(x)],…,fn(x)=f[fn-1(x)],…,考察區間A=(-∞,0),對任意實數x∈A,有f1(x)=f(x)=a<0,f2(x)=f[f1(x)]=f(a)<0,且n≥2時,fn(x)<0,問:是否還有其它區間,對于該區間的任意實數x,只要n≥2,都有fn(x)<0?
【答案】
分析:由函數f
1(x)=f(x),f
2(x)=f[f
1(x)],f
3(x)=f[f
2(x)],…,f
n(x)=f[f
n-1(x)]…知若使f
n(x)<0等價于f[f
n-1(x)]<0,由f(x)<0,得x<0或x>1,則有f
n-1(x)<0或f
n-1(x)>1,依此類推,要使一切n∈N
+,n≥2,都有f
n(x)<0,必須有f
1(x)<0或f
1(x)>1即f(x)<0或f(x)>1的解集即為所求.
解答:解:f(x)<0,即5x
2-5x>0,故x<0或x>1.
∴f
n(x)<0?f[f
n-1(x)]<0?f
n-1(x)<0或f
n-1(x)>1.
要使一切n∈N
+,n≥2,都有f
n(x)<0,必須使f
1(x)<0或f
1(x)>1,
∴f(x)<0或f(x)>1,即5x-5x
2<0或5x-5x
2>1.
解得x<0或x>1或
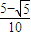
<x<
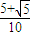
,
∴還有區間(
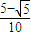
,

)和(1,+∞)
使得對于這些區間內任意實數x,只要n≥2,都有f
n(x)<0
點評:本題一道方案類型題,做題時要用即定的規律進行遞推,轉化,還涉及到不等式的法和恒成立問題.

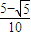 <x<
<x<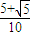 ,
,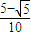 ,
, )和(1,+∞)
)和(1,+∞)

